Matemática - Análise Combinatória

Análise combinatória

Introdução

A análise combinatória é a área da Matemática responsável pela análise das possibilidades e das combinações. É um conjunto de procedimentos que possibilita a construção de grupos, formados por um número finito de elementos de um conjunto sob certas circunstâncias.
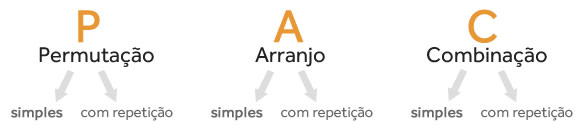
Os três principais tipos de agrupamentos são arranjos, permutações e combinações. Cada um deles pode ser simples ou com elementos repetidos. Neste tópico, estudaremos os agrupamentos simples.
Porém, antes de estudá-los, aprenderemos a seguir o conceito de fatorial.

Fatorial de um número

O fatorial de um número natural n, representado por n!, é o produto de todos os inteiros positivos menores ou iguais a n.
n! = n.(n-1).(n-2)...3.2.1

Definições especiais

0!=1
1!=1

Exemplos


Arranjo simples

Arranjo simples de n elementos tomados p a p, onde n>=1 e p é um número natural, é qualquer ordenação de p elementos dentre os n elementos, em que cada maneira de tomar os elementos se diferenciam pela ordem e natureza dos elementos. A fórmula para cálculo de arranjo simples é dada por:

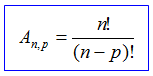
Continuação dos exemplos


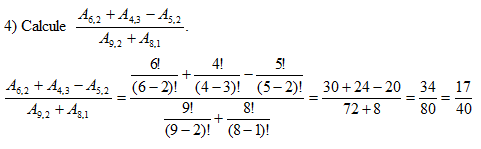
Permutação simples

É um caso particular de arranjo simples. É o tipo de agrupamento ordenado onde entram todos os elementos.

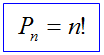
Continuação dos exemplos


Combinação simples

É o tipo de agrupamento em que um grupo difere do outro apenas pela natureza dos elementos componentes.

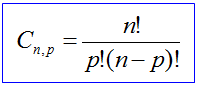
Continuação dos exemplos

Comentários

Postar um comentário

Postagens mais visitadas deste blog

Regras para os cantos litúrgicos / Músicas que não deveriam ser cantadas na Missa

Equipe de Liturgia - Paróquia Divino Espírito Santo – jatiúca – Maceió/AL INTRODUÇÃO:  NOÇÕES GERAIS. Os cantos litúrgicos da missa devem respeitar cada um de seus ritos: ritos iniciais, da palavra, rito eucarístico, rito de comunhão e ritos finais.  Devem ser cantos originais, jamais plágios, paródias ou cópias de cantos não católicos. De preferência, eles devem ter aprovação da igreja. Por exemplo, um erro grave ainda muito cometido em algumas paróquias é o seguinte canto do Pai Nosso: “Ó Pai Nosso, Tu que estás nos que amam a verdade, faz o reino que é teu Senhor...”. Este canto é uma paródia da música tema do filme “A primeira noite de um homem”. Outra paródia pode ser constatada no canto: “É santo, cheio de glória, ó hosana nas alturas. Bendito, aquele que vem entre nós trazendo a mensagem...”. Este canto é uma paródia da música “Hey Jude”, dos Beathles. Na liturgia, classificamos os cantos em dois grandes grupos: os que ACOMPANHAM O RITO e os cantos que s...
Leia mais

Pronúncia de líquido, liquidação e liquidificador

Os principais dicionários (Aulete, Houaiss, Aurélio e Michaelis) e o VOLP, da ABL, aceitam, no caso dessas palavras, a pronúncia ou não do "u". Assim sendo, consideram-se gramaticalmente corretas as seguintes pronúncias, seja com o u mudo, seja com o u pronunciado: líquido (qu) líquido (qü) liquidez (qu) liquidez (qü) liquidar (qu) liquidar (qü) liquidação (qu) liquidação (qü) liquidificador (qu) liquidificador (qü)
Leia mais

Italiano - Conjunções

Conjunções As conjunções -  Le congiunzioni Conjunções são palavras invariáveis que unem duas ou mais palavras em uma oração, ou duas ou mais orações num período. Num texto elas possuem um valor fundamental, o de deixá-lo fluente, coerente, compreensível para seu leitor. Além disso, podem funcionar como pistas para o leitor descobrir, fazer hipóteses durante a sua leitura. Como em português, são divididas em dois grandes grupos: subordinative (subordinadas) e coordinative (coordenadas). Conjunções coordenadas (Congiunzione coordinative) Unem orações independentes, que sintaticamente se equivalem. As conjunções coordenadas se dividem em: Tipos de Conjunções Exemplos Função copulative  (aditivas) e  (e) , anche  (também) , né  (nem), *neppure/ neanche/nemmeno (nem, nem mesmo) indica uma ligação pura e simples disgiuntive  ( disjuntivas) o  (ou) , oppure  (ou melhor) , ovvero  (ou melhor) indica uma separação ou e...
Leia mais