Matemática - Equações Diferenciais
Equações diferenciais
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
| Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação). |
Classificação
- Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
- Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos
y' = 2x
| tem ordem 1 e grau 1 |
| y"+x2(y')3 - 40y = 0 | tem ordem 2 e grau 3 |
y"'+x2y3 = x.tanx
| tem ordem 3 e grau 3 |
Resolução
A solução de uma equação diferencial é uma função que não contém derivadas nem diferenciais e que satisfaz a equação dada (ou seja, a função que, substituída na equação dada, a transforma em uma identidade).
Ex: Equação diferencial ordinária: 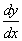 = 3x2 - 4x + 1
= 3x2 - 4x + 1
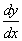 = 3x2 - 4x + 1
= 3x2 - 4x + 1
dy = (3x2 - 4x + 1) dx
y = x3 - 2x2 + x + C (solução geral)
Uma solução particular pode ser obtida da geral através, por exemplo, da condição y(-1) = 3
(condição inicial)
3 = -1 - 2 - 1 + C  C = 7
C = 7  y = x3 - 2x2 + x + 7 (solução particular)
y = x3 - 2x2 + x + 7 (solução particular)
Observação: Em qualquer dos dois casos, a prova pode ser feita derivando a solução e, com isso, voltando à equação dada.
As soluções se classificam em:
Solução geral - apresenta n constantes independentes entre si (n = ordem da EDO). Essas constantes, de acordo com a conveniência, podem ser escritas C, 2C, C2, lnC,
Solução particular - Obtida da geral, mediante condições dadas (chamadas condições iniciais ou condições de contorno).
Equações lineares homogêneas, 2ª ordem
FORMA : y'' + a1y' + a0y = 0 (a0, a1 constantes)
Ex: y = 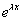
Então y' = 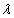
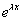 e y'' =
e y'' = 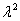
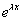
Substituindo na equação dada:
ou
A solução da equação diferencial linear irá depender da raízes 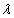 1 e
1 e 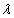 2.
2.
-
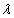 1,
1, 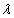 2 números reais e distintos
2 números reais e distintos 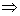 C1
C1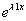 e C2
e C2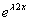 são soluções particulares da EDO e a solução geral é y = C1
são soluções particulares da EDO e a solução geral é y = C1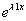 + C2
+ C2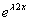
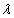 1 =
1 = 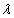 2 =
2 = 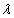 (números reais e iguais)
(números reais e iguais) 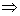 a solução geral da EDO é y = C1
a solução geral da EDO é y = C1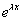 + C2x
+ C2x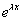
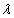 1 = a + bi,
1 = a + bi, 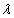 2 = a - bi (complexos conjugados: a, b reais)
2 = a - bi (complexos conjugados: a, b reais) 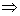 a solução geral é y = C1
a solução geral é y = C1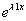 + C2
+ C2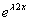
Ex: y'' - 2y' - 15y = 0
Equação característica: 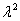 - 2
- 2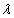 - 15 = 0 cujas raízes são:
- 15 = 0 cujas raízes são: 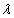 1 = 5,
1 = 5, 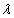 2= -3
2= -3
Solução geral: y = 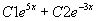
Equações diferenciais lineares de ordem N
Uma equação diferencial linear de ordem n é da forma:
fn(x)y(n) + fn-1(x) y(n-1) +...+ f2(x) y'' + f1(x)y' + f0(x)y = k(x)
onde k(x) e os coeficientes fi (x) são funções de x.
Classificações
Equação linear homogênea (k(x) = 0), ou equação linear não-homogênea (k(x) 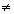 0).
0).
Equação linear:
de coeficientes constantes (f0, f1, f2, ..., fn constantes)
de coeficientes variáveis (pelo menos um fi variável)
de coeficientes variáveis (pelo menos um fi variável)
Equações diferenciais exatas
Se P e Q têm derivadas parciais contínuas, então:
P(x,y)dx + Q(x,y)dy = 0
é uma equação diferencial exata se e somente se
Ex: (3x² - 2y³ + 3)dx + (x³ - 6xy² + 2y)dy = 0
P(x,y) = 3x²y - 2y³ + 3 e Q(x,y) = x³ - 6xy² + 2y
logo Px = Qx e a equação diferencial é exata.
Teorema
A equação diferencial linear de primeira ordem y' + P(x)y = Q(x) pode ser transformada em uma equação diferencial de variáveis separáveis multiplicando-se ambos os membros pelo fator integrante 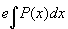 .
.
Ex: 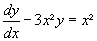
Solução: A equação tem a forma do teorema onde, P(x) = -3x² e Q(x) = x²
Pelo teorema: 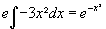
Multiplicando todos os termos pelo fator integrante: 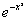
A multiplicação por 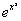 dá a solução:
dá a solução:
Comentários
Postar um comentário