Matemática - Derivadas
Reta Tangente
Para entender o conceito de derivada, primeiramente você precisa saber o que é uma reta tangente.
Fixamos um ponto P no gráfico de uma função f, e escolhemos um Q 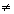 P. Fazendo Q se aproximar de P, pode acontecer que a reta PQ tenda a uma posição-limite: uma reta t.
P. Fazendo Q se aproximar de P, pode acontecer que a reta PQ tenda a uma posição-limite: uma reta t.
Nesse caso, t é chamada reta tangente de f em P, desde que ela não seja vertical. Assim, a reta PQ é chamada de reta secante ao gráfico de f em P.
Podemos observar no gráfico abaixo que Q deve se aproximar de P tanto pela esquerda quanto pela direita, e em ambos os casos a reta PQ deve tender a t (reta verde).
Primeiro gráfico - Pela esquerda
Segundo gráfico - Pela direita
OBS: A reta tangente ao gráfico de uma função nem sempre existe.
A figura abaixo apresenta um exemplo de gráfico onde P é o bico de uma função, sendo assim, o processo descrito anteriormente conduz a duas posições-limites (t1 e t2), obtidas respectivamente ao fazer Q se aproximar de P pela esquerda e pela direita.
Cálculo da inclinação da reta tangente
Consideremos a curva que é o gráfico de uma função contínua f e P(xo, f(xo)) um ponto sobre a curva. Analisaremos agora, o cálculo da inclinação (coeficiente angular) da reta tangente à curva traçada por f no ponto P.
Para analisarmos esta questão, escolhemos um número pequeno 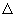 x, diferente de 0, onde
x, diferente de 0, onde 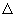 x é o deslocamento no eixo das abscissas. Sobre o gráfico, marcamos o ponto Q(xo +
x é o deslocamento no eixo das abscissas. Sobre o gráfico, marcamos o ponto Q(xo + 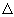 x, f (xo +
x, f (xo + 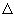 x)). Traçamos uma reta secante que passa pelos pontos P e Q.
x)). Traçamos uma reta secante que passa pelos pontos P e Q.
A inclinação (coeficiente angular) desta reta é dada da seguinte maneira:
Derivada
Definição
A derivada de uma função y = f(x) num ponto x = x0, é igual ao valor da tangente trigonométrica do ângulo formado pela tangente geométrica à curva representativa de y=f(x), no ponto x = x0, ou seja, a derivada é o coeficiente angular da reta tangente ao gráfico da função no ponto x0.
A derivada de uma função y = f(x), pode ser representada também pelos símbolos:
y', dy/dx ou f ' (x).
y', dy/dx ou f ' (x).
A derivada de uma função f(x) no ponto x0 é dada por:
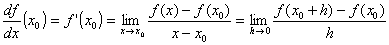
Algumas derivadas básicas
Nas fórmulas abaixo, u e v são funções da variável x.
a, b, c e n são constantes.
Derivada de uma constante
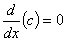
Derivada da potência
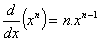
Portanto:
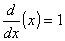
Soma / Subtração
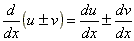
Produto por uma constante
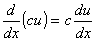
Derivada do produto
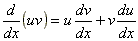
Derivada da divisão
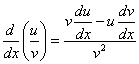
Potência de uma função
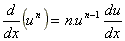
Derivada de uma função composta
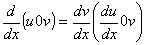
Regra da cadeia
Com as regras que temos à nossa disposição até o presente momento, não conseguimos calcular alguns tipos de derivadas.
Veremos agora a regra da cadeia, uma fórmula para a derivada da função composta de duas funções. Criada por Gottfried Leibniz, a regra da cadeia teve grande importância para o avanço do cálculo diferencial.
A fórmula é a seguinte:
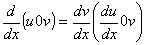
Ela pode ser escrita como:
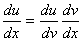
Outra fórmula similar é a seguinte:
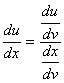
Exemplo
Calcular 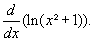
Procedemos do seguinte modo:
Escrevemos y = ln (x² + 1). Com a esperança de usar a derivada de ln, faremos:
u = x² + 1
y = ln u
y = ln u
Calculamos:
Usamos a regra da cadeia, cujo primeiro membro é a derivada procurada:
ou seja, multiplicando as derivadas obtidas no passo anterior:
Usamos agora a expressão de u que é (x² + 1), para obter
Derivada da função inversa
A inversa da função y(x) é a função x(y):
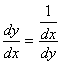
Derivadas de funções trigonométricas e suas inversas
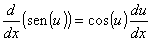
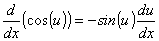
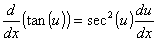
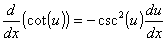
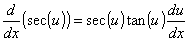
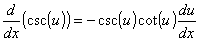
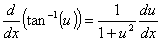
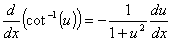
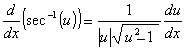
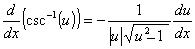
Derivadas de funções exponencial e logarítmica
Derivada do logaritmo natural
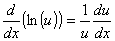
Derivada do logaritmo em outras bases
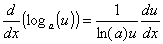
Exponencial
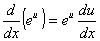
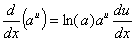
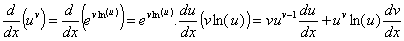
Lembre-se da definição da função logarítmica com base a > 0:
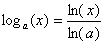
Derivadas das funções hiperbólicas e suas inversas
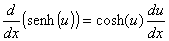
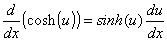
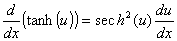
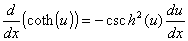
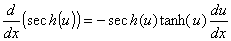
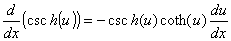
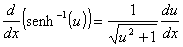
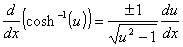
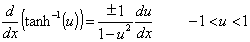
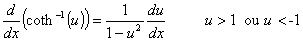
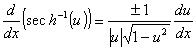
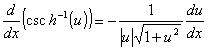
Lembre-se das definições das funções trigonométricas:
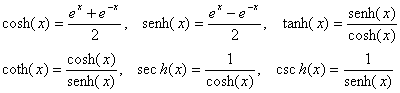
Derivadas de alta ordem
Seja y = f(x). Temos:
A segunda derivada é dada por:
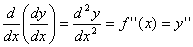
A terceira derivada é dada por:
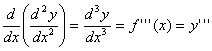
A enésima derivada é dada por:
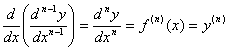
Em alguns livros, a seguinte notação também é usada:
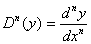
Comentários
Postar um comentário