Matemática - Função Afim
Função do 1º grau
Definição
Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a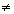 0.
0.
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
f(x) = 5x - 3, onde a = 5 e b = - 3f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a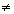 0, é uma reta oblíqua aos eixos Ox e Oy. Por exemplo, vamos construir o gráfico da função y = 3x - 1:
0, é uma reta oblíqua aos eixos Ox e Oy. Por exemplo, vamos construir o gráfico da função y = 3x - 1:
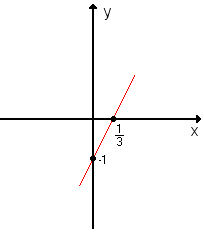
Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
a) Para x = 0, temos y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1).
b) Para y = 0, temos 0 = 3x - 1; portanto,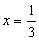 e outro ponto é
e outro ponto é 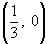 .
.
b) Para y = 0, temos 0 = 3x - 1; portanto,
Marcamos os pontos (0, -1) e 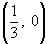 no plano cartesiano e ligamos os dois com uma reta.
no plano cartesiano e ligamos os dois com uma reta.
| x | y |
| 0 | -1 |
| 0 |
Já vimos que o gráfico da função afim y = ax + b é uma reta.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, está ligado à inclinação da reta em relação ao eixo Ox.
O termo constante, b, é chamado coeficiente linear da reta. Para x = 0, temos y = a · 0 + b = b. Assim, o coeficiente linear é a ordenada do ponto em que a reta corta o eixo Oy.
Zero ou raiz da função do 1º grau
Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a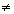 0, o número real x tal que f(x) = 0. Temos:
0, o número real x tal que f(x) = 0. Temos:
f(x) = 0  ax + b = 0
ax + b = 0 
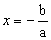
Vejamos alguns exemplos:
- Obtenção do zero da função f(x) = 2x - 5:
f(x) = 0 2x - 5 = 0
2x - 5 = 0 
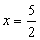
- Cálculo da raiz da função g(x) = 3x + 6:
g(x) = 0 3x + 6 = 0
3x + 6 = 0  x = -2
x = -2
- Cálculo da abscissa do ponto em que o gráfico de h(x) = -2x + 10 corta o eixo das abscissas:O ponto em que o gráfico corta o eixo dos x é aquele em que h(x) = 0; então:
h(x) = 0 -2x + 10 = 0
-2x + 10 = 0  x = 5
x = 5
Função crescente ou decrescente
Consideremos a função do 1º grau y=3x-1. Vamos atribuir valores cada vez maiores a x e observar o que ocorre com y:
| ||||||||||||||||

Regra geral:
- a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
- a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
- a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
Justificativa:
- para a > 0: se x1 < x2, então ax1 < ax2. Daí, ax1 + b < ax2 + b, de onde vem f(x1) < f(x2).
- para a < 0: se x1 < x2, então ax1 > ax2. Daí, ax1 + b > ax2 + b, de onde vem f(x1) > f(x2).
Sinal da função do 1º grau
Estudar o sinal de qualquer função y = f(x) é determinar os valor de x para os quais y é positivo, os valores de x para os quais y é zero e os valores de x para os quais y é negativo.
Considerando uma função afim y = f(x) = ax + b, vamos estudar seu sinal. Já vimos que essa função se anula pra raiz 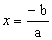 . Há dois casos possíveis:
. Há dois casos possíveis:
1º) a > 0 (a função é crescente)
y > 0  ax + b > 0
ax + b > 0  x >
x > 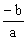
y < 0  ax + b < 0
ax + b < 0  x <
x < 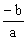
Conclusão: y é positivo para valores de x maiores que a raiz; y é negativo para valores de x menores que a raiz
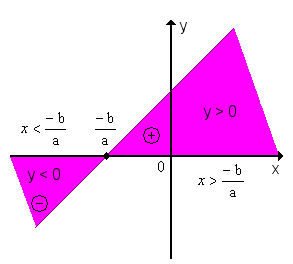
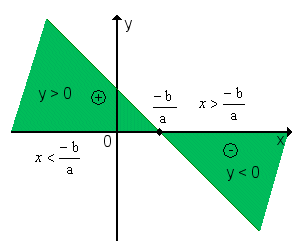
2º) a < 0 (a função é decrescente)
y > 0  ax + b > 0
ax + b > 0  x <
x < 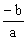
y < 0  ax + b < 0
ax + b < 0  x >
x > 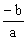
Conclusão: y é positivo para valores de x menores que a raiz; y é negativo para valores de x maiores que a raiz.
Comentários
Postar um comentário