Matemática - Funções Logarítmica e Exponencial
Funções Logarítmica e Exponencial
Antes de estudarmos estes dois tipos de funções, vamos entender o que são funções inversas.
Funções inversas
Em linguagem comum, o termo "inversão" transmite a ideia de uma reversão. Por exemplo, em meteorologia, a inversão da temperatura é uma reversão nas propriedades usuais da temperatura de camadas de ar; em música, uma inversão é um tema recorrente que usa as mesmas notas na ordem reversa. Em matemática, o termo inversa é usado para descrever funções que são reversas uma da outra, no sentido que cada uma desfaz o efeito da outra.
A ideia de resolver uma equação y = f (x) para x com uma função de y, digamos x = g(y), é uma das ideias mais importantes da matemática. Às vezes, resolver esta equação é um processo simples; por exemplo usando álgebra básica, a equação
pode ser resolvida para x como uma função de y:
A primeira equação é melhor para calcular y se x for conhecido, e a segunda é melhor para calcular x se y for conhecido
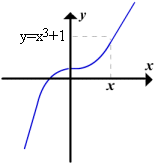
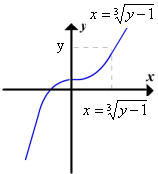
O interesse fundamental é identificar relações que possam existir entre as funções f e g, quando uma função y=f(x) for expressa como x = g(y), ou ao contrário. Por exemplo, consideremos as funções 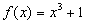 e
e 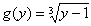 discutidas acima. Quando funções forem compostas em qualquer ordem, uma cancela o efeito da outra significando que
discutidas acima. Quando funções forem compostas em qualquer ordem, uma cancela o efeito da outra significando que
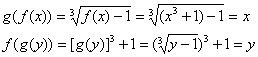
A primeira dessas equações estabelece que cada saída de uma composição g(f(x)) é igual à entrada, e a segunda estabelece que cada saída da composição f(g(y)) é igual à entrada. Os pares de funções com essas duas propriedades são tão importantes que há uma terminologia específica para elas.
| Se as funções f e g satisfazem as duas condições
g(f(x)) = x para todo x no domínio de f
f(g(y)) = y para todo y no domínio de g
então, dizemos que f e g são funções inversas. Além disso, chamamos f uma inversa de g e g uma inversa de f.
|
Exemplo
Confirme cada um dos seguintes itens.
(a) A inversa de 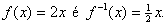
(b) A inversa de 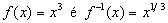
Solução (a).
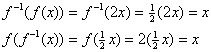
Solução (b).
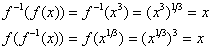
OBSERVAÇÃO. O resultado no exemplo deve fazer sentido intuitivamente para você, uma vez que as operações de multiplicar por 2 e multiplicar por 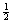 em qualquer ordem cancelam uma o efeito da outra, da mesma que as operações de elevar ao cubo e extrair a raiz cúbica.
em qualquer ordem cancelam uma o efeito da outra, da mesma que as operações de elevar ao cubo e extrair a raiz cúbica.
Domínio e imagem das funções inversas
A equação seguinte:
|
f (
|
implica em certas relações entre os domínios e as imagens de f e 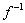 . Por exemplo, na primeira equação a quantidade f (x) é uma entrada de
. Por exemplo, na primeira equação a quantidade f (x) é uma entrada de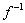 , assim pontos nas imagens de f estão no domínio de
, assim pontos nas imagens de f estão no domínio de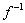 ; e na segunda equação, a quantidade
; e na segunda equação, a quantidade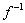 (x)é uma entrada de f, sendo que pontos na imagem de
(x)é uma entrada de f, sendo que pontos na imagem de 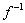 estão no domínio de f. Tudo isso sugere as seguintes relações:
estão no domínio de f. Tudo isso sugere as seguintes relações:
| domínio de
imagem de
|
Uma vez que f e g satisfazem duas condições:
- g(f(x)) = x para todo x no domínio de f
- f(g(y)) = y para todo y no domínio de g
concluímos que elas são inversas. Assim temos o seguinte resultado.
| Se uma equação y = f (x) pode ser resolvida para x como uma função de y, então f tem uma inversa e a equação resultante é x = |
Um método para achar inversas
Exemplo
Ache a inversa de f (x) = 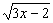
Solução. Podemos achar uma fórmula para 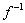 (y) resolvendo a equação
(y) resolvendo a equação
y = 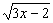
para x como uma função de y. Os cálculos são:
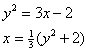
da qual tem-se que
Até aqui, fomos bem-sucedidos em obter uma fórmula para 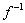 ; contudo não estamos realmente completos, uma vez que não há nenhuma garantia de que o domínio natural associado é o domínio completo para
; contudo não estamos realmente completos, uma vez que não há nenhuma garantia de que o domínio natural associado é o domínio completo para 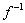 .
.
Para determinar se isto é o que acontece, examinaremos a imagem de y = f (x) = 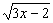 . A imagem consiste de todos os y no intervalo
. A imagem consiste de todos os y no intervalo 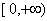 , assim este intervalo é também o domínio de
, assim este intervalo é também o domínio de 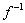 (y); logo a inversa de f é dada pela fórmula
(y); logo a inversa de f é dada pela fórmula
OBSERVAÇÃO. Quando uma fórmula para 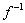 for obtida resolvendo-se a equação y = f(x) para x como uma função de y, a fórmula resultante tem y como a variável independente. Se for preferível ter x como a variável independente para
for obtida resolvendo-se a equação y = f(x) para x como uma função de y, a fórmula resultante tem y como a variável independente. Se for preferível ter x como a variável independente para 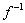 , então há duas formas: você pode resolver y = f(x) para x com uma função de y, e então substituir y por x na fórmula final para
, então há duas formas: você pode resolver y = f(x) para x com uma função de y, e então substituir y por x na fórmula final para 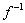 , ou então você pode trocar x e y na equação original e resolver a equação x = f(y) para y em termos de x. Neste caso a equação final será y =
, ou então você pode trocar x e y na equação original e resolver a equação x = f(y) para y em termos de x. Neste caso a equação final será y = 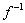 (x).
(x).
Gráfico das funções inversas
O próximo objetivo é explorar as relações entre os gráficos de f e 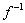 . Com esse propósito, será desejável usar x como a variável independente para ambas as funções, o que significa estarmos comparando os gráficos de y = f(x) e y =
. Com esse propósito, será desejável usar x como a variável independente para ambas as funções, o que significa estarmos comparando os gráficos de y = f(x) e y = 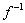 (x).
(x).
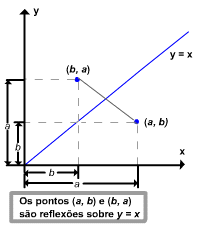
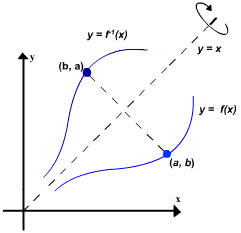
Se (a,b) for um ponto no gráfico y = f(x), então b = f(a). Isto é equivalente à afirmativa que a = 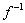 (b), a qual significa que (b,a) é um ponto no gráfico de y =
(b), a qual significa que (b,a) é um ponto no gráfico de y = 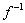 (x).
(x).
Em resumo, inverter as coordenadas de um ponto no gráfico de f produz um ponto no gráfico de 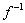 . Analogamente inverter as coordenadas de um ponto no gráfico de
. Analogamente inverter as coordenadas de um ponto no gráfico de 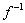 produz um ponto no gráfico de f . Contudo, o efeito geométrico de inverter as coordenadas de um ponto é refletir aquele ponto sobre a reta y = x (figura 1), e logo os gráficos de y = f(x) e y =
produz um ponto no gráfico de f . Contudo, o efeito geométrico de inverter as coordenadas de um ponto é refletir aquele ponto sobre a reta y = x (figura 1), e logo os gráficos de y = f(x) e y = 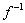 (x) são um do outro em relação a esta reta (figura 2). Resumindo, temos o seguinte resultado.
(x) são um do outro em relação a esta reta (figura 2). Resumindo, temos o seguinte resultado.
| Se f tiver uma inversa, então os gráficos de y = f(x) e y = |
Funções crescentes ou decrescentes têm inversas
Se o gráfico da função f for sempre crescente ou sempre decrescente sobre o domínio de f, então este gráfico pode ser cortado, no máximo, uma vez por qualquer reta horizontal e, conseqüentemente, a função f deve ter uma inversa.
Uma forma de dizer se o gráfico de uma função é crescente ou decrescente em um intervalo é pelo exame das inclinações de suas retas tangentes. O gráfico de f deve ser crescente em qualquer intervalo, onde f'(x)>0 (uma vez que as retas tangentes têm inclinação positiva) e deve ser decrescente em qualquer intervalo onde f'(x)<0 (uma vez que as retas tangentes têm inclinação negativa). Essas observações sugerem o seguinte teorema.
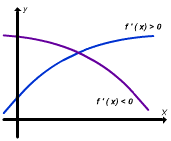
| Se o domínio de f for um intervalo no qual f' (x)>0 ou no qual f'(x)<0, então a função f tem uma inversa. |
Exemplo
O gráfico de f(x) = 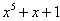 é sempre crescente em
é sempre crescente em 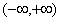 , uma vez que
, uma vez que
para todo x. Contudo, não há maneira fácil de resolver a equação y = 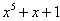 para x em termos de y; mesmo sabendo que f tem uma inversa, não podemos produzir uma fórmula para ela.
para x em termos de y; mesmo sabendo que f tem uma inversa, não podemos produzir uma fórmula para ela.
OBSERVAÇÃO. O que é importante entender aqui é que a nossa incapacidade de achar uma fórmula para a inversa não nega a sua existência; de fato, é necessário que se desenvolvam formas de achar propriedades de funções, as quais não têm fórmula explícita para se trabalhar com elas.
Funções logarítmica e exponencial
Quando os logaritmos foram introduzidos no século XVII como uma ferramenta computacional, eles forneceram aos cientistas daquela época um poder de cálculo até então inimaginável.
Embora os computadores e as calculadoras tenham substituído amplamente os logaritmos em cálculos numéricos, as funções logarítmica e suas relativas tem uma vasta aplicação na matemática e na ciência.
Expoentes irracionais
Em álgebra, as potências inteiras e racionais de um número b estão definidas por
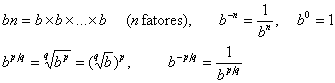
Se b for negativo, então algumas das potências fracionárias de b terão valores imaginários; por exemplo, 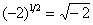 . Para evitar esta complicação, vamos supor que
. Para evitar esta complicação, vamos supor que 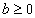 , mesmo que não seja estabelecido explicitamente.
, mesmo que não seja estabelecido explicitamente.
Observe que as definições precedentes não incluem potências irracionais de b, tais como
Há vários métodos para definir potências irracionais. Uma abordagem é definir potências irracionais de b como limite de potências racionais. Por exemplo, para definir 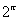 devemos começar com a representação decimal de
devemos começar com a representação decimal de 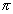 , isto é,
, isto é,
3,1415926
Desta decimal, podemos formar uma seqüência de números racionais que ficam cada vez mais próximos de 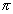 isto é,
isto é,
3,1; 3,14; 3,141; 3,1415; 3,14159
e a partir destes podemos formar uma seqüência de potências racionais de 2:
Uma vez que os expoentes dos termos desta seqüência tendem a um limite 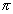 , parece plausível que os próprios termos tendam a um limite; sendo assim, é razoável definir
, parece plausível que os próprios termos tendam a um limite; sendo assim, é razoável definir 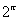 como sendo este limite. A tabela abaixo fornece evidência numérica de que a seqüência, na realidade, tem um limite e para quatro casas decimais, o valor deste limite é
como sendo este limite. A tabela abaixo fornece evidência numérica de que a seqüência, na realidade, tem um limite e para quatro casas decimais, o valor deste limite é 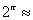 8,8250. Em geral, para qualquer expoente irracional p e número positivo b, podemos definir
8,8250. Em geral, para qualquer expoente irracional p e número positivo b, podemos definir 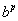 como o limite de potências racionais de b, criadas pela expansão decimal de p.
como o limite de potências racionais de b, criadas pela expansão decimal de p.
Tabela
| x | |
| 3 | 8,000000 |
| 3,1 | 8,574188 |
| 3,14 | 8,815241 |
| 3,141 | 8,821353 |
| 3,1415 | 8,824411 |
| 3,14159 | 8,824962 |
| 3,141592 | 8,824974 |
A família de funções exponenciais
Uma função da forma f (x) = 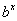 , onde b > 0 e b
, onde b > 0 e b 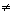 1, é chamada de função exponencial de base b, cujos exemplos são
1, é chamada de função exponencial de base b, cujos exemplos são
f (x) = 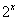 , f (x) =
, f (x) = 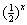 , f (x) =
, f (x) = 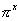
Note que uma função exponencial tem uma base constante e um expoente variável. Assim as funções tais como f (x) = 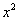 e f (x) =
e f (x) = 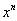 não seriam classificadas como funções exponenciais, uma vez que elas tem uma base variável e um expoente constante.
não seriam classificadas como funções exponenciais, uma vez que elas tem uma base variável e um expoente constante.
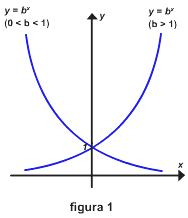
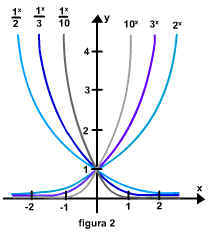
Pode ser mostrado que as funções exponenciais são contínuas e têm um dos dois aspectos básicos mostrados na figura 1, dependendo de se 0 < b < 1 ou b > 1. A figura 2 mostra os gráficos de algumas funções exponenciais específicas.
OBSERVAÇÃO. Se b = 1, então a função 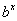 é constante, uma vez que
é constante, uma vez que 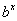 =
= 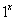 = 1. Este caso não é de nosso interesse aqui, assim o excluímos da família das funções exponenciais.
= 1. Este caso não é de nosso interesse aqui, assim o excluímos da família das funções exponenciais.
Logaritmos
Lembre-se que, algebricamente, o logaritmo é um expoente. Mais precisamente, se b > 0 e b 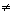 1, então para valores positivos de x o logaritmo na base b de x é denotado por
1, então para valores positivos de x o logaritmo na base b de x é denotado por
e é definido como sendo aquele expoente ao qual b deve ser elevado para produzir x. Por exemplo,
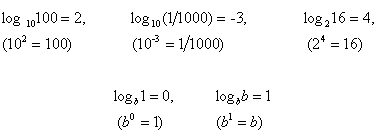
Historicamente, os primeiros logaritmos a serem estudados foram os de base 10 chamados de logaritmos comuns. Para tais logaritmos, é usual suprimir referência explícita para a base e escrever log x e não 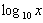 . Mais recentemente, os logaritmos de base dois desempenharam importante papel em ciência computacional, uma vez que surgem naturalmente em sistema numérico binário.
. Mais recentemente, os logaritmos de base dois desempenharam importante papel em ciência computacional, uma vez que surgem naturalmente em sistema numérico binário.
Porém, os logaritmos mais largamente usados nas aplicações são logaritmos naturais, os quais tem uma base natural denotada pela letra e em homenagem ao matemático suíço Leonard Euler, que primeiro sugeriu sua aplicação aos logaritmos no artigo não-publicado, escrito em 1728. Esta constante, cujo valor está em seis casas decimais, é
e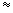 2, 718282
2, 718282
surge como assíntota horizontal ao gráfico da equação
y = 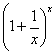
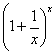
Os valores de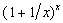 aproximam-se a e
aproximam-se a e
| x | 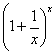 | |
| 1 | 2 | |
| 10 | 1,1 | 2,593742 |
| 100 | 1,01 | 2,704814 |
| 1000 | 1,001 | 2,716924 |
| 10.000 | 1,0001 | 2,718146 |
| 100.000 | 1,00001 | 2,718268 |
| 1.000.000 | 1,000001 | 2,718280 |
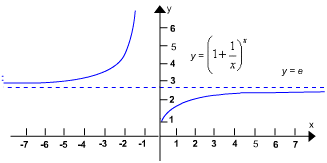
O fato de que y = e, quando x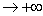 e quando x
e quando x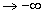 é expresso pelos limites
é expresso pelos limites
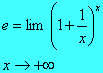 e
e 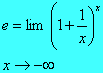
A função exponencial f (x) = 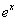 é chamada de função exponencial natural. Para simplificar a tipografia, esta função é, algumas vezes, escrita como exp x. Assim, por exemplo, você pode ver a relação
é chamada de função exponencial natural. Para simplificar a tipografia, esta função é, algumas vezes, escrita como exp x. Assim, por exemplo, você pode ver a relação 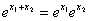 expressa como
expressa como
exp(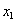 +
+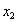 ) = exp(
) = exp(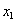 ) exp(
) exp(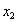 )
)
Esta notação é também usada por recursos computacionais, e é típico acessar a função 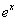 com alguma variação do comando EXP.
com alguma variação do comando EXP.
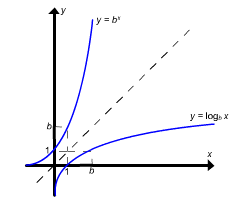
Funções logarítmicas
A figura 1 abaixo sugere que se b > 0 e b 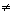 1, então o gráfico de y =
1, então o gráfico de y = 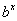 satisfaz o teste da reta horizontal, e isso implica que a função f (x) =
satisfaz o teste da reta horizontal, e isso implica que a função f (x) = 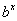 tem uma inversa.
tem uma inversa.

Para encontrar uma fórmula para esta inversa (com x como variável independente), podemos resolver a equação x = 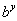 para y com uma função de x. Isto pode ser feito tomando o logaritmo na base de b de ambos os lados desta equação. Isto dá lugar a
para y com uma função de x. Isto pode ser feito tomando o logaritmo na base de b de ambos os lados desta equação. Isto dá lugar a
Porém, se pensarmos 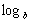 (
(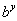 ) como expoente ao qual b se deve ser elevado para produzir
) como expoente ao qual b se deve ser elevado para produzir 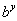 , então fica evidente que
, então fica evidente que 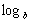 (
(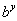 ). Assim, pode ser reescrito como
). Assim, pode ser reescrito como
y = 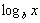
de onde concluímos que a inversa de f (x) = 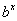 é
é 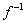 (x) =
(x) = 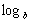 x. Isto implica que o gráfico de x =
x. Isto implica que o gráfico de x = 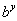 e o de y =
e o de y = 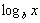 são reflexões um do outro, em relação relação à reta y = x.
são reflexões um do outro, em relação relação à reta y = x.
Chamaremos 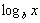 de função logarítmica na base b.
de função logarítmica na base b.
Em particular, se tomarmos f (x) = 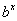 e
e 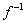 (x) =
(x) = 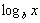 , e se tivermos em mente que o domínio de
, e se tivermos em mente que o domínio de 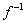 é o mesmo que a imagem de f, então obtemos
é o mesmo que a imagem de f, então obtemos
| logb(bx)=x para todos os valores reais de x blog x=x para x>0 |
Em outras palavras, a equação nos diz que as funções logb(bx) e blog x cancelam o efeito de outra quando compostas em qualquer ordem; por exemplo
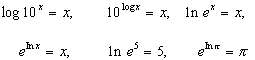
Funções definidas explicitamente e implicitamente
Até agora, estávamos preocupados em diferenciar funções que são expressas na forma y = f (x). Dizemos que uma equação desta forma define y explicitamente como uma função de x, pois a variável y aparece sozinha de um lado da equação. Entretanto, algumas vezes as funções estão definidas com equações nas quais y não está sozinho de um lado; por exemplo, a equação
yx + y +1 = x
não está na forma y = f (x). Contudo, esta equação ainda define y como uma função de x, uma vez se pode reescrever como
y =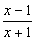
Assim dizemos que xy + y +1 = x define y implicitamente como uma função de x, sendo
f (x) = 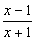
Uma equação em x e y pode implicitamente definir mais do que uma função de x; por exemplo, se resolvermos a equação
para y em termos de x, obtemos 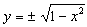 ; assim, encontramos duas funções que estão definidas implicitamente por
; assim, encontramos duas funções que estão definidas implicitamente por 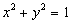 , isto é
, isto é
Os gráficos destas funções são semicírculos superiores e inferiores do círculo 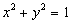 .
.
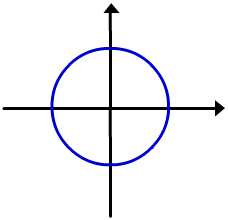
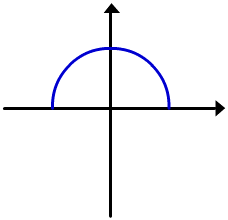 y=
y=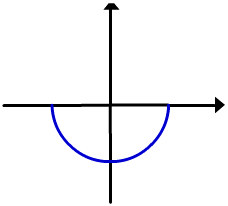 y = -
y = -
Em geral, se tivermos uma equação em x e y, então qualquer segmento de seu gráfico que passe pelo teste vertical pode ser visto como gráfico de una função definida pela equação. Assim fazemos a seguinte definição:
| Definição. Dizemos que uma dada equação em x e y define a função f implicitamente se o gráfico de y = f (x) coincidir com algum segmento do gráfico da equação. |
Assim, por exemplo, a equação 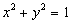 define as funções
define as funções 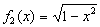 e
e 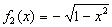 implicitamente, uma vez que os gráficos dessas funções são os segmentos do círculo
implicitamente, uma vez que os gráficos dessas funções são os segmentos do círculo 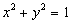 .
.
Às vezes, pode ser difícil ou impossível resolver uma equação em x e y para y em termos de x.
Com persistência, a equação
por exemplo, pode ser resolvida para y em termos de x, mas a álgebra é enfadonha e as fórmulas resultantes são complicadas. Por outro lado, a equação
sen(xy) = y
não pode ser resolvida para y em termos de x por qualquer método elementar. Assim, mesmo que uma equação em x e y possa definir uma ou mais funções de x, pode não ser prático ou possível achar fórmulas explícitas para aquelas funções.
Diferenciação implícita
Em geral, não é necessário resolver uma equação de y em termos de x, a fim de diferenciar as funções definidas pela equação. Para ilustrar isto, consideremos a equação
xy = 1
Uma maneira de achar dy/dx é reescrever esta equação como
da qual tem-se que
Contudo, há uma outra maneira de obter esta derivada. Podemos diferenciar ambos os lados de xy = 1 antes de resolver para y em termos de x, tratando y como (não-especificado temporariamente) uma função diferenciável de x. Com esta abordagem, obtemos
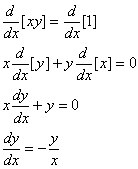
Se agora substituirmos 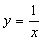 na última expressão, obtemos
na última expressão, obtemos
que está de acordo com 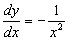 . Este método para obter derivadas é chamado de diferenciação implícita.
. Este método para obter derivadas é chamado de diferenciação implícita.
Exemplo 1
Use a diferenciação implícita para achar dy/dx se 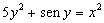
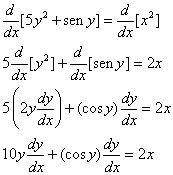
Resolvendo para dy/dx obtemos
Note que esta fórmula envolve ambos x e y. A fim de obter uma fórmula para dy/dx que envolva apenas x, teríamos que resolver a equação original para y em termos de x e, então, substituir em 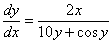 . Entretanto, isto é impossível de ser feito; assim, somos forçados a deixar a fórmula dy/dx em termos de x e y.
. Entretanto, isto é impossível de ser feito; assim, somos forçados a deixar a fórmula dy/dx em termos de x e y.
Exemplo 2
Use a diferenciação implícita para achar 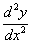 se
se 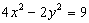 .
.
Solução. Diferenciado ambos os lados de 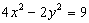 implicitamente, obtém-se
implicitamente, obtém-se
de que obtemos
Diferenciando ambos os lados de 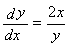 implicitamente, obtém-se
implicitamente, obtém-se
Substituindo 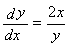 dentro de
dentro de 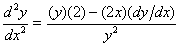 e simplificando, usando a equação original, obtemos
e simplificando, usando a equação original, obtemos
Nos Exemplos 1 e 2, os resultados das fórmulas para dy/dx envolvem ambos x e y. Embora seja usualmente mais desejável ter a fórmula para dy/dx expressa somente em termos de x, ter a fórmula em termos de x e y não é um impedimento para achar as inclinações e as equações das retas tangentes, desde que as coordenadas x e y do ponto de tangência sejam conhecidas.
Derivadas de potências racionais de x
A partir da equação que segue, mostramos que a fórmula
é válida para todos os valores inteiros de n e para n = 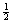 . Usaremos agora a diferenciação implícita para mostrar que esta fórmula é válida para qualquer expoente racional. Mais precisamente, mostraremos que se r for um número racional, então
. Usaremos agora a diferenciação implícita para mostrar que esta fórmula é válida para qualquer expoente racional. Mais precisamente, mostraremos que se r for um número racional, então
sempre que 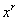 e
e 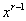 estiverem definidas. Por ora, admitiremos, sem prova que
estiverem definidas. Por ora, admitiremos, sem prova que 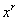 é diferenciável.
é diferenciável.
Seja y = 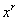 . Uma vez que r é um número racional, pode ser expresso como uma razão de inteiros r = m/n. Assim, y =
. Uma vez que r é um número racional, pode ser expresso como uma razão de inteiros r = m/n. Assim, y = 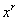 =
= 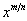 pode ser escrito como
pode ser escrito como
Diferenciando implicitamente em relação a x e usando 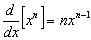 , obtemos
, obtemos
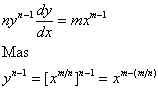
Desta forma, pode ser escrito como
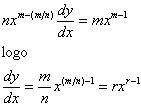
Exemplo
A partir de 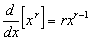
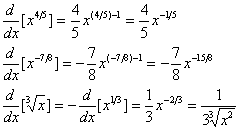
Se u for uma função diferenciável de x e r for um número racional, então a regra da cadeia dá lugar à seguinte generalização de 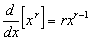
Derivadas de funções logarítmicas
Agora, obteremos fórmulas das derivadas para as funções logarítmicas e exponenciais e discutiremos as relações gerais entre e derivada de uma função um a um e a sua inversa.
O logaritmo natural desempenha um papel especial no cálculo que pode ser motivado diferenciando 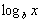 , onde b é uma base arbitrária. Para esta proposta, admitiremos que
, onde b é uma base arbitrária. Para esta proposta, admitiremos que 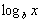 é diferenciável, e portanto contínua para x > 0. Também necessitaremos do limite
é diferenciável, e portanto contínua para x > 0. Também necessitaremos do limite
Usando a definição de derivada, obtemos(com x em vez de v como variável).
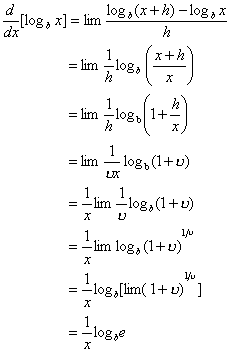
Assim,
Mas a partir da fórmula , temos 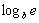 = 1/1n b; logo, podemos reescrever esta fórmula de derivada como
= 1/1n b; logo, podemos reescrever esta fórmula de derivada como
No caso especial onde b = e, temos 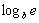 = 1n e = 1, logo esta fórmula torna-se
= 1n e = 1, logo esta fórmula torna-se
Assim, entre todas as possíveis bases, a base b = e produz a fórmula mais simples da derivada para 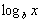 . Esta é uma das razões por que a função do logaritmo natural é preferida sobre todos os logaritmos no cálculo.
. Esta é uma das razões por que a função do logaritmo natural é preferida sobre todos os logaritmos no cálculo.
Exemplo 1
Ache 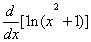
Solução. A partir de 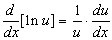
Quando possível as propriedades dos logaritmos devem ser usadas para converter produtos, quocientes e expoentes em somas, em diferenças e em múltiplos de constantes, antes de diferenciar uma função envolvendo logaritmos.
Exemplo 2
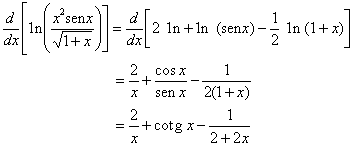
Diferenciação logarítmica
Consideremos agora uma técnica chamada diferenciação logarítmica, a qual é útil para diferenciar funções compostas de produtos, de quocientes e de potências.
Exemplo
A derivada de
é relativamente difícil de ser calculada diretamente. Contudo, se primeiro tomarmos o logaritmo natural de ambos os lados e, então, usarmos suas propriedades, podemos escrever:
Diferenciando ambos os lados em relação a x, resulta
Assim, resolvendo para dy/dx e usando 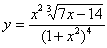 obtemos
obtemos
OBSERVAÇÃO.Uma vez que 1n y é definido apenas para y > 0, a diferenciação logarítmica de y = f(x) é válida apenas nos intervalos onde f(x) for positiva. Assim, a derivada mostrada no exemplo é válida no intervalo ( 2, +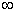 ), uma vez que a função dada é positiva para x > 2. Contudo, a fórmula é realmente válida também no intervalo ( -
), uma vez que a função dada é positiva para x > 2. Contudo, a fórmula é realmente válida também no intervalo ( -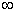 , 2). Isso pode ser visto tomando-se valores absolutos antes de prosseguir com a diferenciação logarítmica e notando que
, 2). Isso pode ser visto tomando-se valores absolutos antes de prosseguir com a diferenciação logarítmica e notando que 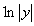 está definido para todo y exceto em y = 0. Se fizermos isso e simplificarmos usando as propriedades de logaritmos e dos valores absolutos, obteremos
está definido para todo y exceto em y = 0. Se fizermos isso e simplificarmos usando as propriedades de logaritmos e dos valores absolutos, obteremos
Diferenciando ambos os lados em relação a x dá lugar a , e, portanto, resulta em .Em geral, se a derivada de y = f(x) for obtida por diferenciação logarítmica, então a mesma fórmula para dy/dx resultará tomando-se ou não, primeiro, valores absolutos. Assim, uma fórmula da derivada obtida por diferenciação logarítmica será válida, exceto nos pontos onde f(x) for zero. A fórmula pode ser válida também naqueles pontos, mas não é garantido.
Derivadas das funções exponenciais
Para obter uma fórmula para a derivada de funções exponenciais
y = 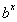
reescrevemos esta equação como
x = 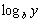
e diferenciamos implicitamente usando 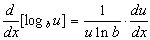 para obter
para obter
que podemos reescrever usando y = 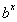 como
como
Assim, mostrando que se 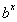 for uma função diferenciável, então sua derivada em relação a x é
for uma função diferenciável, então sua derivada em relação a x é
No caso especial onde b = e temos 1n e = 1n, assim 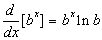 torna-se
torna-se
Além disso, se u for uma função diferenciável de x, então tem-se a partir de 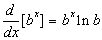 e
e 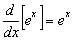 que
que
OBSERVAÇÃO.É importante distinguir entre diferenciar 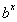 (expoente variável e base constante) e
(expoente variável e base constante) e 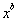 (base variável e expoente constante).
(base variável e expoente constante).
Exemplo
Os cálculos a seguir usam 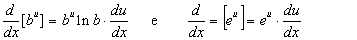
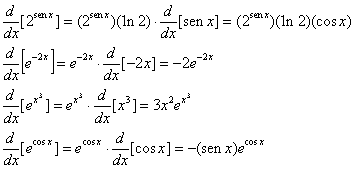
Derivadas das funções trigonométricas inversas
Um problema comum em trigonometria é achar um ângulo cujas funções trigonométricas são conhecidas.
Problemas deste tipo envolvem a computação de funções arco, tais como arcsen x, arccos x, arctg x, e assim por diante. Consideremos esta ideia do ponto de vista de funções inversas, com a meta de desenvolver fórmulas de derivadas para as funções trigonométricas inversas.
Identidades para funções trigonométricas inversas
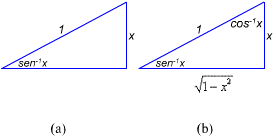
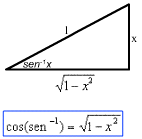
Se interpretamos 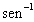 x como um ângulo medido em radianos cujo seno é x, e se aquele ângulo for não negativo, então podemos representar
x como um ângulo medido em radianos cujo seno é x, e se aquele ângulo for não negativo, então podemos representar 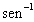 x como um ângulo em um triângulo retângulo, no qual a hipotenusa tem comprimento 1 e o lado oposto ao ângulo de
x como um ângulo em um triângulo retângulo, no qual a hipotenusa tem comprimento 1 e o lado oposto ao ângulo de 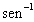 tem comprimento x (figura a). Pelo Teorema de Pitágoras, o lado adjacente para o ângulo
tem comprimento x (figura a). Pelo Teorema de Pitágoras, o lado adjacente para o ângulo 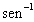 tem comprimento
tem comprimento 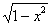 .
.
Além disso, o ângulo oposto a 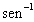 é
é 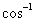 , uma vez que o co-seno daquele ângulo é x (figura b). Este triângulo motiva várias identidades úteis, envolvendo funções trigonométricas que são válidas para
, uma vez que o co-seno daquele ângulo é x (figura b). Este triângulo motiva várias identidades úteis, envolvendo funções trigonométricas que são válidas para 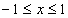 . Por exemplo:
. Por exemplo:
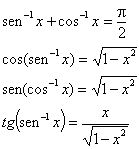
Analogamente, 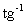 x e
x e 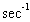 x podem ser representadas com ângulos de triângulos retângulos mostrados na figura c e d. Esses triângulos revelam mais identidades úteis, como por exemplo:
x podem ser representadas com ângulos de triângulos retângulos mostrados na figura c e d. Esses triângulos revelam mais identidades úteis, como por exemplo:
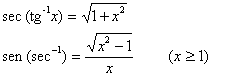
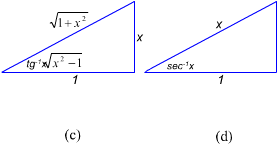
OBSERVAÇÃO. Não se ganha nada memorizando estas identidades; o que é importante é compreender o método usado para obtê-las.
Exemplo
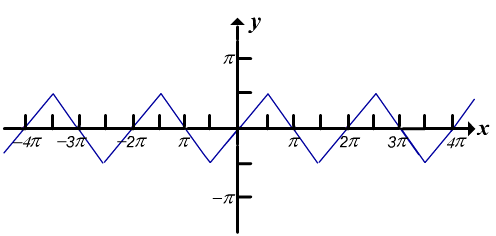
A figura abaixo mostra um gráfico gerado por um computador de y = 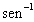 (sen x). Pode se pensar que este gráfico deva ser a reta y = x, uma vez que
(sen x). Pode se pensar que este gráfico deva ser a reta y = x, uma vez que 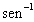 (sen x) = x. Por que isto não acontece?
(sen x) = x. Por que isto não acontece?
Solução. A relação 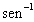 (sen x) = x é válida no intervalo
(sen x) = x é válida no intervalo 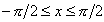 ; logo podemos dizer, com certeza, que os gráficos de y =
; logo podemos dizer, com certeza, que os gráficos de y = 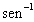 (sen x) e y = x coincidem neste intervalo. Contudo, fora deste intervalo, a relação
(sen x) e y = x coincidem neste intervalo. Contudo, fora deste intervalo, a relação 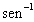 (sen x) = x não precisa ser válida. Por exemplo, se estiver no intervalo
(sen x) = x não precisa ser válida. Por exemplo, se estiver no intervalo 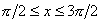 , então a quantidade x -
, então a quantidade x - 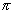 estará no intervalo
estará no intervalo 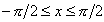 . Assim
. Assim
Desta forma,usando a identidade sen(x-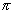 ) = -sen x e o fato de que
) = -sen x e o fato de que 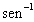 é uma função ímpar, podemos expressar
é uma função ímpar, podemos expressar 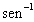 (sen x) como
(sen x) como
Isso mostra que no intervalo 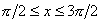 , o gráfico de y =
, o gráfico de y = 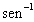 (sen x) coincide com a reta y = -(x-
(sen x) coincide com a reta y = -(x-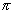 ), a qual tem inclinação -1 e um intercepto x em x =
), a qual tem inclinação -1 e um intercepto x em x = 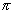 , o que está de acordo com a figura.
, o que está de acordo com a figura.
Fórmula de derivação
Lembre-se que se f for uma função um a um, cuja a derivada é conhecida, então há duas maneiras básicas para obter uma fórmula de derivação para 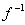 (x), podemos reescrever a equação y =
(x), podemos reescrever a equação y = 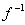 (x) como x = f(y), e diferenciar implicitamente. Usaremos a diferenciação implícita para obter a fórmula de derivação para y =
(x) como x = f(y), e diferenciar implicitamente. Usaremos a diferenciação implícita para obter a fórmula de derivação para y = 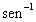 x. Reescrevendo esta equação como x = sen y e diferenciando implicitamente, obtemos
x. Reescrevendo esta equação como x = sen y e diferenciando implicitamente, obtemos
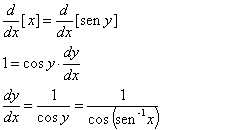
Esta fórmula de derivada pode ser simplificada aplicando-se a fórmula 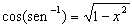 , que foi deduzida a partir do triângulo da figura, resultando:
, que foi deduzida a partir do triângulo da figura, resultando:
Assim, mostramos que
Se u for uma função diferenciável de x, então 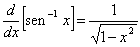 e a regra da cadeia produzem a seguinte fórmula generalizada da derivada
e a regra da cadeia produzem a seguinte fórmula generalizada da derivada
O método usado para obter esta fórmula pode também ser usado para obter fórmulas generalizadas de derivadas para outras funções trigonométricas inversas. Estas fórmulas, válidas para -1< u < 1, são
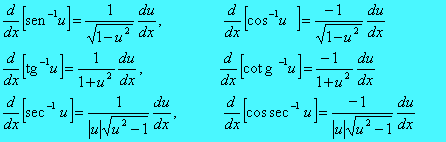
Comentários
Postar um comentário