Matemática - Geometria Analítica (Cônicas)
Geometria analítica - Cônicas
Introdução
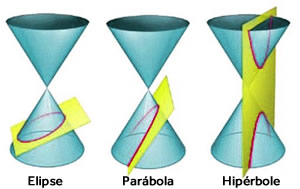
Chamamos de cônicas as curvas geradas ou encontradas na intersecção de um plano que atravessa um cone. Estudaremos as seguintes cônicas:
- Elipse: definida na interseção de um plano que atravessa a superfície de um cone. Também é usada na gramática, para definir uma figura de linguagem, mais especificamente uma figura de construção ou sintática que consiste na omissão de um termo facilmente subentendido pelo contexto, e quando este já apareceu antes e quer-se evitar a repetição, recebe o nome de zeugma;
- Parábola: também definida na intersecção de um plano que penetra a superfície de um cone. Também é usada na religião, para definir uma narrativa alegórica que evoca, por comparação, valores de ordem superior, encerra lições de vida e pode conter preceitos morais ou religiosos, encontrada especialmente nos textos dos Evangelhos;
- Hipérbole: definida na interseção de um plano que penetra num cone em paralelo ao seu eixo. Também é usada na gramática, para definir uma figura de linguagem, mais especificamente uma figura de pensamento, que consiste no emprego de uma expressão exagerada para dar mais expressividade à mensagem.
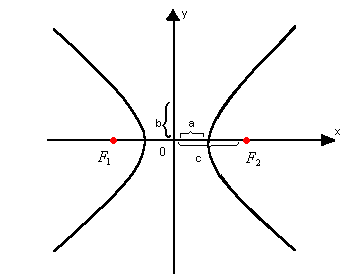
Elipse
Considerando, num plano 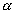 , dois pontos distintos, F1 e F2 e, sendo 2a um número real maior que a distância entre F1 e F2, chamamos de elipse o conjunto dos pontos do plano
, dois pontos distintos, F1 e F2 e, sendo 2a um número real maior que a distância entre F1 e F2, chamamos de elipse o conjunto dos pontos do plano 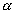 tais que a soma das distâncias desses pontos a F1 e F2 seja sempre igual a 2a.
tais que a soma das distâncias desses pontos a F1 e F2 seja sempre igual a 2a.
Por exemplo, sendo P, Q, R, S, F1 e F2 pontos de um mesmo plano e F1F2 < 2a, temos:
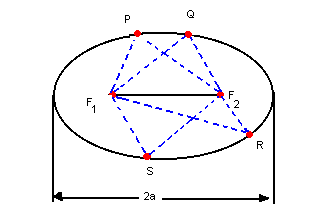
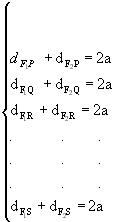
A figura obtida é uma elipse. Observações:
1ª) A Terra descreve uma trajetória elíptica em torno do sol, que é um dos focos dessa trajetória. A lua em torno da terra e os demais satélites em relação a seus respectivos planetas também apresentam esse comportamento.
2ª) O cometa de Halley segue uma órbita elíptica, tendo o Sol como um dos focos.
3ª) As elipses são chamadas cônicas porque ficam configuradas pelo corte feito em um cone circular reto por um plano oblíquo em relação à sua base.
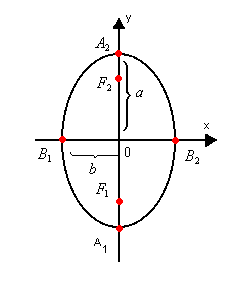
Elementos
Observe a elipse a seguir. Nela, consideramos os seguintes elementos:
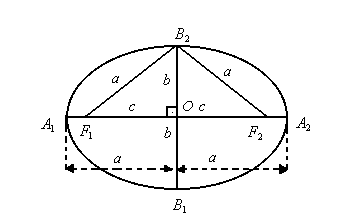
- focos : os pontos F1 e F2
- centro: o ponto O, que é o ponto médio de
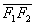
- semi-eixo maior: a
- semi-eixo menor: b
- semidistância focal: c
- vértices: os pontos A1, A2, B1, B2
- eixo maior:
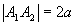
- eixo menor:
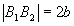
- distância focal:
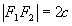
Relação fundamental
Na figura acima, aplicando o Teorema de Pitágoras ao triângulo OF2B2 , retângulo em O, podemos escrever a seguinte relação fundamental:
a2 =b2 + c2
|
Excentricidade
Chamamos de excentricidade o número real e tal que:
Pela definição de elipse, 2c < 2a, então c < a e, consequentemente, 0 < e < 1.
Observação: quando os focos são muito próximos, ou seja, c é muito pequeno, a elipse se aproxima de uma circunferência.
Equações da elipse
Vamos considerar os seguintes casos:
a) elipse com centro na origem e eixo maior horizontal
Sendo c a semidistância focal, os focos da elipse são F1(-c, 0) e F2(c, 0):
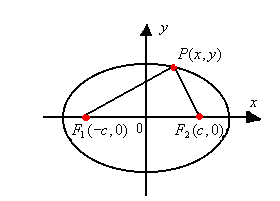
Aplicando a definição de elipse 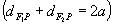 , obtemos a equação da elipse:
, obtemos a equação da elipse:
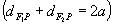 , obtemos a equação da elipse:
, obtemos a equação da elipse:b) elipse com centro na origem e eixo maior vertical
Nessas condições, a equação da elipse é:
Hipérbole
Considerando, num plano 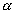 , dois pontos distintos, F1 e F2 e, sendo 2a um número real menor que a distância entre F1 e F2, chamamos de hipérbole o conjunto dos pontos do plano
, dois pontos distintos, F1 e F2 e, sendo 2a um número real menor que a distância entre F1 e F2, chamamos de hipérbole o conjunto dos pontos do plano 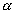 tais que o módulo da diferença das distâncias desses pontos a F1 e F2 seja sempre igual a 2a.
tais que o módulo da diferença das distâncias desses pontos a F1 e F2 seja sempre igual a 2a.
Por exemplo, sendo P, Q, R, S, F1 e F2 pontos de um mesmo plano e F1F2 = 2c, temos:
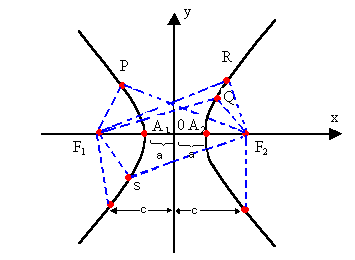
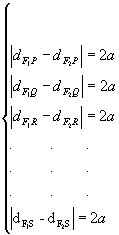
A figura obtida é uma hipérbole.
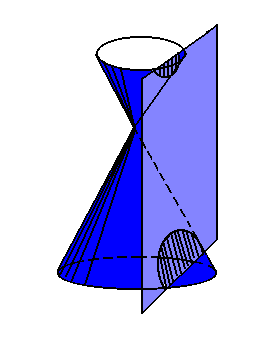
Observação: os dois ramos da hipérbole são determinados por um plano paralelo ao eixo de simetria de dois cones circulares retos e opostos pelo vértice:
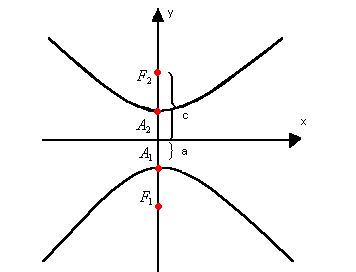
Elementos
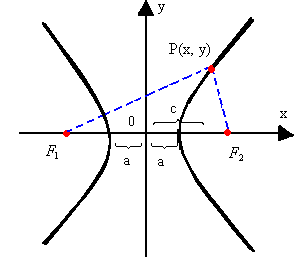
Observe a hipérbole representada a seguir. Nela, temos os seguintes elementos:
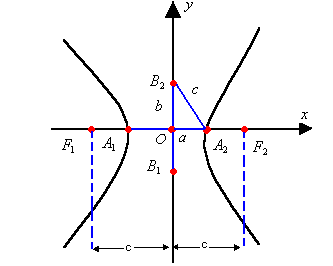
- focos: os pontos F1 e F2
- vértices: os pontos A1 e A2
- centro da hipérbole: o ponto O, que é o ponto médio de
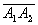
- semi-eixo real: a
- semi-eixo imaginário: b
- semidistância focal: c
- distância focal:
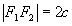
- eixo real:

- eixo imaginário:
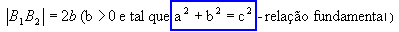
Excentricidade
Chamamos de excentricidade o número real e tal que:
Como c > a, temos e > 1.
Equações da hipérbole
Vamos considerar os seguintes casos:
a) hipérbole com centro na origem e focos no eixo Ox
F1 (-c, 0)
F2 (c, 0)
F2 (c, 0)
Aplicando a definição de hipérbole:
Obtemos a equação da hipérbole:
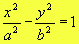
b) hipérbole com centro na origem e focos no eixo Oy
Nessas condições, a equação da hipérbole é:
Hipérbole equilátera
Uma hipérbole é chamada equilátera quando as medidas dos semi-eixos real e imaginário são iguais:
a = b
Assíntotas da hipérbole
Assíntotas são retas que contêm as diagonais do retângulo de lados 2a e 2b.
Quando o eixo real é horizontal, o coeficiente angular dessas retas é 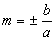 ; quando é vertical, o coeficiente é
; quando é vertical, o coeficiente é 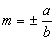 .
.
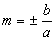 ; quando é vertical, o coeficiente é
; quando é vertical, o coeficiente é 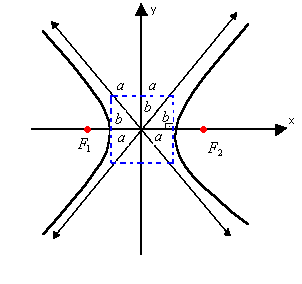
Equação
Vamos considerar os seguintes casos:
a) eixo real horizontal e C(0, 0)
As assíntotas passam pela origem e têm coeficiente angular 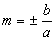 ; logo, suas equações são da forma:
; logo, suas equações são da forma:
b) eixo vertical e C(0, 0)
As assíntotas passam pela origem e têm coeficiente angular 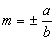 ; logo, suas equações são da forma:
; logo, suas equações são da forma:
Parábola
Dados uma reta d e um ponto F 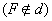 , de um plano
, de um plano 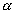 , chamamos de parábola o conjunto de pontos do plano
, chamamos de parábola o conjunto de pontos do plano 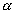 equidistantes de F e d.
equidistantes de F e d.
Por exemplo, sendo F, P, Q e R pontos de um plano 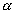 e d uma reta desse mesmo plano, de modo que nenhum ponto pertença a d, temos:
e d uma reta desse mesmo plano, de modo que nenhum ponto pertença a d, temos:
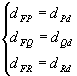
Observações:
1ª) A parábola é obtida seccionando-se obliquamente um cone circular reto:
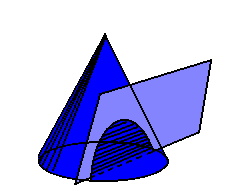
2ª) Os telescópios refletores mais simples têm espelhos com secções planas parabólicas.
3ª) As trajetórias de alguns cometas são parábolas, sendo que o Sol ocupa o foco.
4ª) A superfície de um líquido contido em um cilindro que gira em torno de seu eixo com velocidade constante é parabólica.
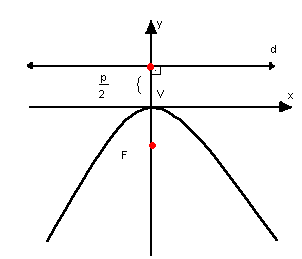
Elementos
Observe a parábola representada a seguir. Nela, temos os seguintes elementos:
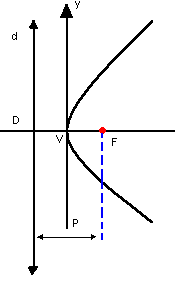
- foco: o ponto F
- diretriz: a reta d
- vértice: o ponto V
- parâmetro: p
Então, temos que:
- o vértice V e o foco F ficam numa mesma reta, o eixo de simetria e.
Assim, sempre temos 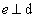 .
.
- DF =p
- V é o ponto médio de
Equações da parábola
Vamos considerar os seguintes casos:
a) parábola com vértice na origem, concavidade para a direita e eixo de simetria horizontal
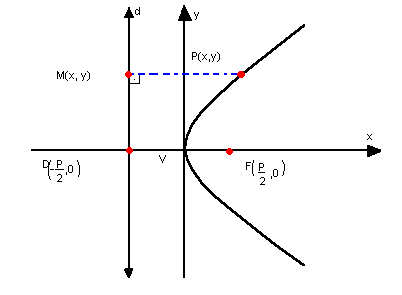
Como a reta d tem equação 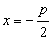 e na parábola temos:
e na parábola temos:
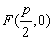 ;
;- P(x, y);
- dPF = dPd ( definição);
obtemos, então, a equação da parábola:
y2 = 2px
|
b) parábola com vértice na origem, concavidade para a esquerda e eixo de simetria horizontal
Nessas condições, a equação da parábola é:
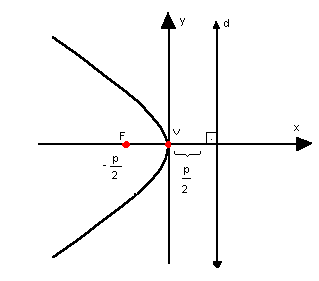
y2 = -2px
|
c) parábola com vértice na origem, concavidade para cima e eixo de simetria vertical
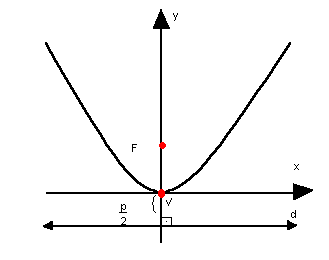
x2=2py
|
d) parábola com vértice na origem, concavidade para baixo e eixo de simetria vertical
| x2= - 2py |
Comentários
Postar um comentário