Matemática - Geometria Espacial (3)
Secção
Secção transversal é a região determinada pela intersecção do cilindro com um plano paralelo às bases. Todas as secções transversais são congruentes.
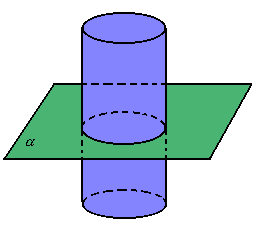
Secção meridiana é a região determinada pela intersecção do cilindro com um plano que contém o eixo.
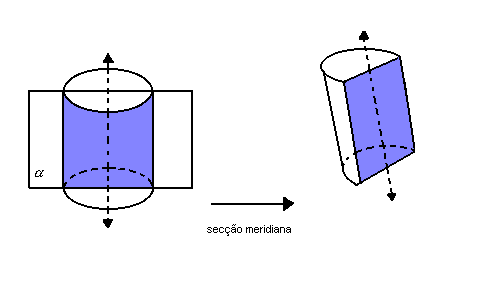
Área do cilindro
Em um cilindro, consideramos as seguintes áreas:
a) área lateral (AL)
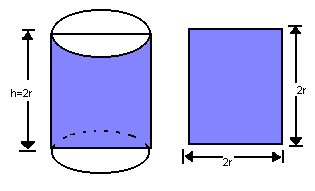
Podemos observar a área lateral de um cilindro fazendo a sua planificação:
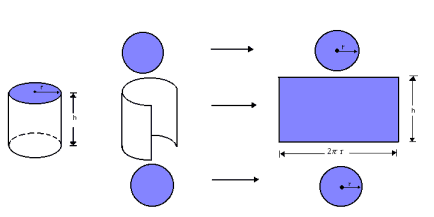
Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões 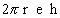 :
:
b) área da base (AB): área do círculo de raio r.
c) área total (AT): soma da área lateral com as áreas das bases.
Volume do cilindro
Para obter o volume do cilindro, vamos usar novamente o princípio de Cavalieri. Dados dois sólidos com mesma altura e um plano  , se todo plano
, se todo plano 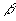 , paralelo ao plano
, paralelo ao plano  , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais:
, intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais:
Se 1 é um paralelepípedo retângulo, então V2 = ABh. Assim, o volume de todo paralelepípedo retângulo e de todo cilindro é o produto da área da base pela medida de sua altura:
| Vcilindro = ABh |
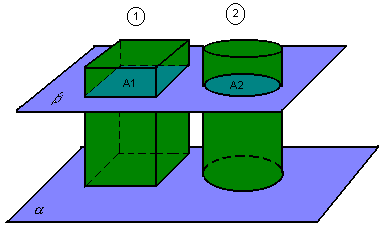
No caso do cilindro circular reto, a área da base é a área do círculo de raio r: 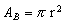 . Portanto, seu volume é:
. Portanto, seu volume é:
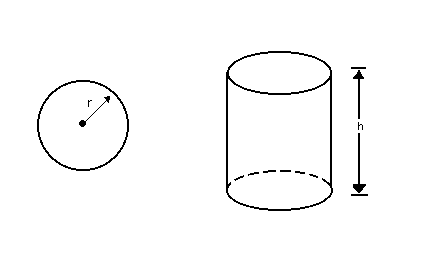
Cilindro equilátero
Todo cilindro cuja secção meridiana é um quadrado (altura igual ao diâmetro da base) é chamado cilindro equilátero.
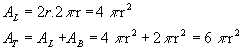
Cone circular
Dado um círculo C, contido num plano  , e um ponto V (vértice) fora de
, e um ponto V (vértice) fora de  , chamamos de cone circular o conjunto de todos os segmentos
, chamamos de cone circular o conjunto de todos os segmentos 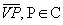 .
.
 , e um ponto V (vértice) fora de
, e um ponto V (vértice) fora de  , chamamos de cone circular o conjunto de todos os segmentos
, chamamos de cone circular o conjunto de todos os segmentos 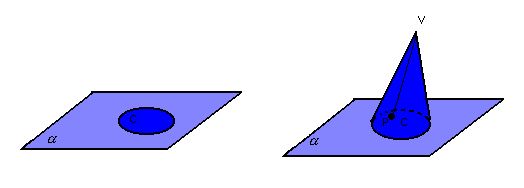
Elementos do cone circular
Dado o cone a seguir, consideramos os seguintes elementos:
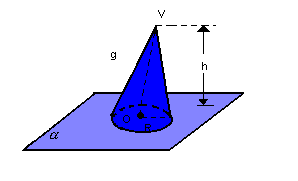
- altura: distância h do vértice V ao plano
 .
. - geratriz (g): segmento com uma extremidade no ponto V e outra num ponto da circunferência.
- raio da base: raio R do círculo.
- eixo de rotação: reta
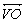 determinada pelo centro do círculo e pelo vértice do cone.
determinada pelo centro do círculo e pelo vértice do cone.
Cone reto
Todo cone cujo eixo de rotação é perpendicular à base é chamado cone reto, também denominado cone de revolução. Ele pode ser gerado pela rotação completa de um triângulo retângulo em torno de um de seus catetos.
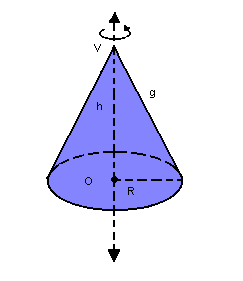
Da figura, e pelo Teorema de Pitágoras, temos a seguinte relação:
| g2 = h2 + R2 |
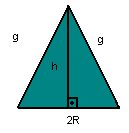
Secção meridiana
A secção determinada, num cone de revolução, por um plano que contém o eixo de rotação é chamada secção meridiana.
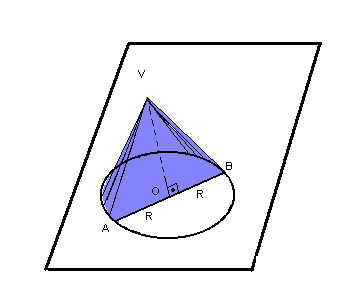
Se o triângulo AVB for equilátero, o cone também será equilátero:
Área e volume do cone
Área
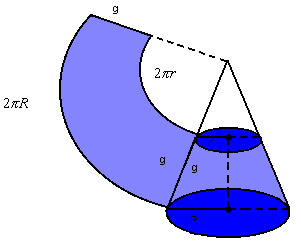
Desenvolvendo a superfície lateral de um cone circular reto, obtemos um setor circular de raio g e comprimento 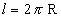 :
:
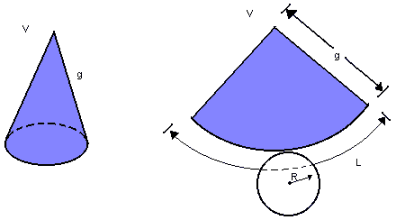
Assim, temos de considerar as seguintes áreas:
a) área lateral (AL): área do setor circular.
b) área da base (AB): área do circulo do raio R.
c) área total (AT): soma da área lateral com a área da base.
Volume
Para determinar o volume do cone, vamos ver como calcular volumes de sólidos de revolução. Observe a figura:
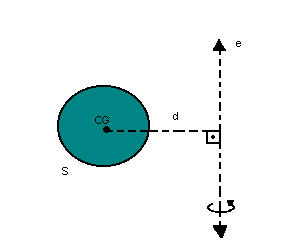
d = distância do centro de gravidade (CG) da sua superfície ao eixo e
S=área da superfície
Sabemos, pelo Teorema de Pappus-Guldin, que, quando uma superfície gira em torno de um eixo e, gera um volume tal que:
Vamos então determinar o volume do cone de revolução gerado pela rotação de um triângulo retângulo em torno do cateto h:
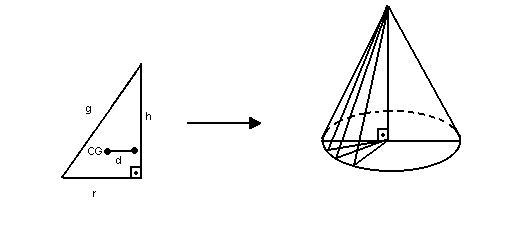
O CG do triângulo está a uma distância 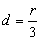 do eixo de rotação. Logo:
do eixo de rotação. Logo:
Pirâmide
Dados um polígono convexo R, contido em um plano  , e um ponto V (vértice) fora de
, e um ponto V (vértice) fora de  , chamamos de pirâmide o conjunto de todos os segmentos
, chamamos de pirâmide o conjunto de todos os segmentos 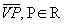 .
.
 , e um ponto V (vértice) fora de
, e um ponto V (vértice) fora de  , chamamos de pirâmide o conjunto de todos os segmentos
, chamamos de pirâmide o conjunto de todos os segmentos 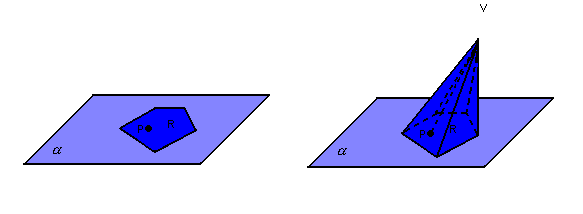
Elementos da pirâmide
Dada a pirâmide a seguir, temos os seguintes elementos:
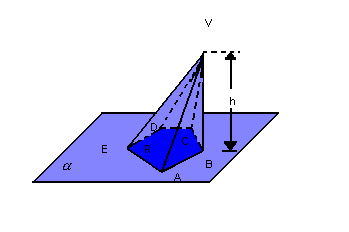
- base: o polígono convexo R.
- arestas da base: os lados
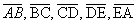 do polígono.
do polígono. - arestas laterais: os segmentos
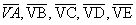 .
. - faces laterais: os triângulos VAB, VBC, VCD, VDE, VEA.
- altura: distância h do ponto V ao plano.
Classificação
Uma pirâmide é reta quando a projeção ortogonal do vértice coincide com o centro do polígono da base. Toda pirâmide reta, cujo polígono da base é regular, recebe o nome de pirâmide regular. Ela pode ser triangular, quadrangular, pentagonal etc., conforme sua base seja, respectivamente, um triângulo, um quadrilátero, um pentágono etc. Veja:
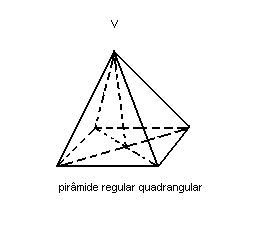
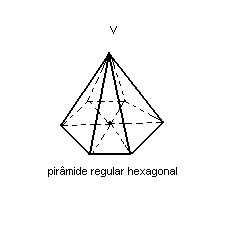
Observações:
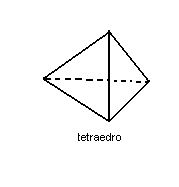
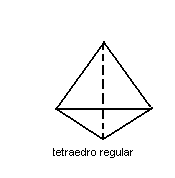
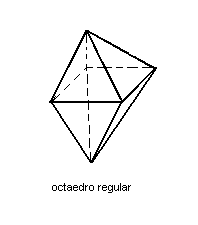
1ª) Toda pirâmide triangular recebe o nome do tetraedro. Quando o tetraedro possui como faces triângulos equiláteros, ele é denominado regular (todas as faces e todas as arestas são congruentes).
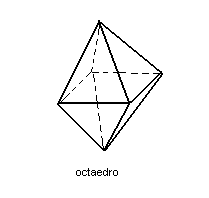
2ª) A reunião, base com base, de duas pirâmides regulares de bases quadradas resulta num octaedro. Quando as faces das pirâmides são triângulos equiláteros, o octaedro é regular.
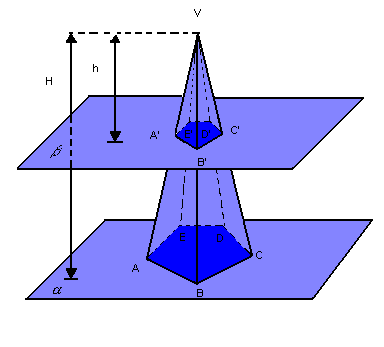
Secção paralela à base de uma pirâmide
Um plano paralelo à base que intercepte todas as arestas laterais determina uma secção poligonal de modo que:
- as arestas laterais e a altura sejam divididas na mesma razão;
- a secção obtida e a base sejam polígonos semelhantes;
- as áreas desses polígonos estejam entre si assim como os quadrados de suas distâncias ao vértice.
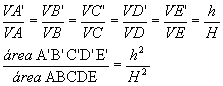
Relações entre os elementos de uma pirâmide regular
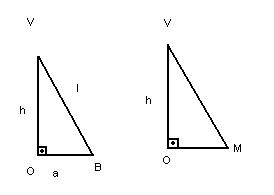
Vamos considerar uma pirâmide regular hexagonal, de aresta lateral l e aresta da base a:
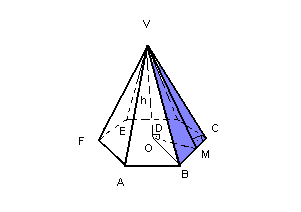
Assim, temos:
- A base da pirâmide é um polígono regular inscritível em um círculo de raio OB = R.
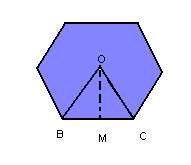

- A face lateral da pirâmide é um triângulo isósceles.
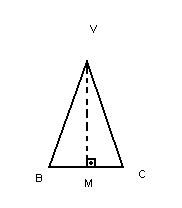
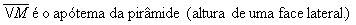
- Os triângulos VOB e VOM são retângulos.
Área e volume da pirâmide
Área
Numa pirâmide, temos as seguintes áreas:
a) área lateral (AL): reunião das áreas das faces laterais.
b) área da base (AB): área do polígono convexo (base da pirâmide).
c) área total (AT): união da área lateral com a área da base.
AT = AL +AB
Para uma pirâmide regular, temos:
em que:

Volume
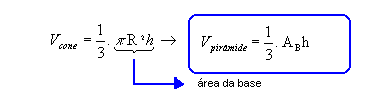
O princípio de Cavalieri assegura que um cone e uma pirâmide equivalentes possuem volumes iguais:
Tronco de pirâmide
Se um plano interceptar todas as arestas de uma pirâmide, paralelamente às suas bases, dividirá o sólido em dois outros: uma nova pirâmide e um tronco de pirâmide. Dado o tronco de pirâmide regular a seguir, temos:
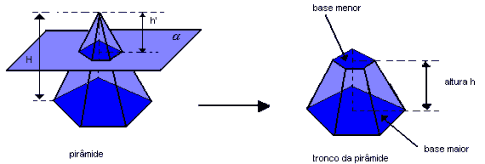
- as bases são polígonos regulares paralelos e semelhantes;
- as faces laterais são trapézios isósceles congruentes.
Áreas
Temos as seguintes áreas:
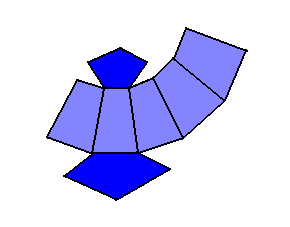
a) área lateral (AL): soma das áreas dos trapézios isósceles congruentes que formam as faces laterais.
b) área total (AT): soma da área lateral com a soma das áreas da base menor (Ab) e maior (AB).
| AT =AL+AB+Ab |
Volume
O volume de um tronco de pirâmide regular é dado por:
Sendo V o volume da pirâmide e V' o volume da pirâmide obtido pela secção, é válida a relação:
Tronco de cone
Se um plano interceptar todas as arestas de um cone, paralelamente às suas bases, dividirá o sólido em dois outros: um novo cone e um tronco de cone. Sendo o tronco do cone circular regular a seguir, temos:
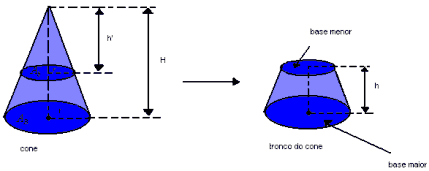
- as bases maior e menor são paralelas;
- a altura do tronco é dada pela distância entre os planos que contém as bases.
Áreas
Temos:
a) área lateral
b) área total
Volume
Sendo V o volume do cone e V' o volume do cone obtido pela secção, são válidas as relações:
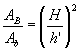
Esfera
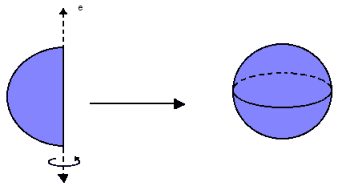
Chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R.
Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior.
Volume
O volume da esfera de raio R é dado por:
Superfície esférica
A superfície esférica de centro O e raio R é o conjunto de pontos do espaço cuja distância ao ponto O é igual ao raio R.
Se considerarmos a rotação completa de uma semicircunferência em torno de seu diâmetro, a superfície esférica é o resultado dessa rotação.
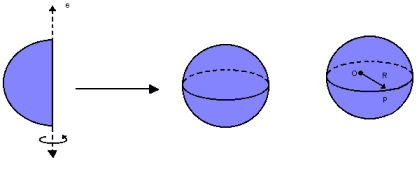
A área da superfície esférica é dada por:
Outras partes da esfera
Zona esférica
É a parte da esfera gerada do seguinte modo:
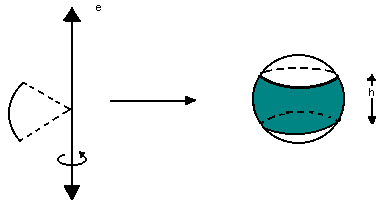
A área da zona esférica é dada por:
Calota esférica
É a parte da esfera gerada do seguinte modo:
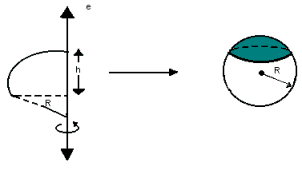
A área da calota esférica é dada por:
Fuso esférico
O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semicircunferência de um ângulo 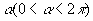 em torno de seu eixo:
em torno de seu eixo:
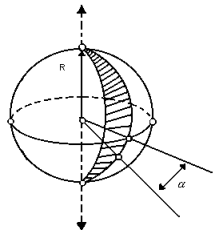
A área do fuso esférico pode ser obtida por uma regra de três simples:
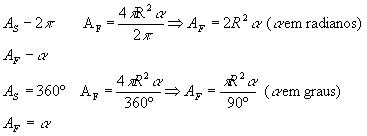
Cunha esférica
Parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo 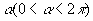 :
:
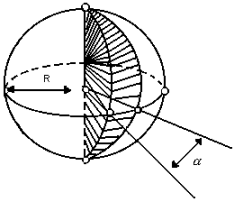
O volume da cunha pode ser obtido por uma regra de três simples:
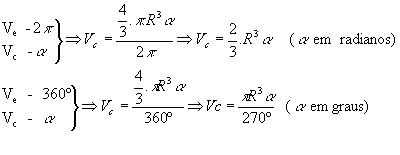
Comentários
Postar um comentário