Matemática - Geometria Espacial

Geometria espacial

Pontos, retas e planos

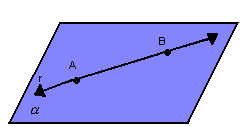
Na geometria espacial, são conceitos primitivos (e, portanto, aceitos sem definição) os conceitos de ponto, reta e plano. Habitualmente, usamos a seguinte notação:

• pontos: letras maiúsculas do nosso alfabeto 

• retas: letras minúsculas do nosso alfabeto

   

• planos: letras minúsculas do alfabeto grego

Observação: Espaço é o conjunto de todos os pontos.

Por exemplo, da figura a seguir, podemos escrever:

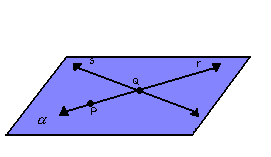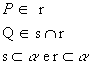Axiomas

Axiomas, ou postulados (P), são proposições aceitas como verdadeiras sem demonstração e que servem de base para o desenvolvimento de uma teoria. Temos como axioma fundamental: existem infinitos pontos, retas e planos.

Postulados sobre pontos e retas

P1) A reta é infinita, ou seja, contém infinitos pontos.

P2) Por um ponto podem ser traçadas infinitas retas.

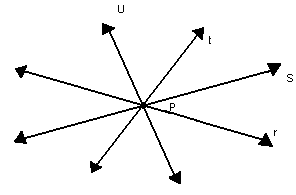
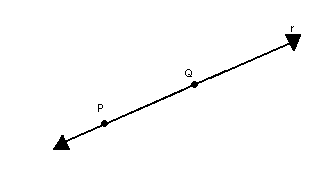
P3) Por dois pontos distintos passa uma única reta.

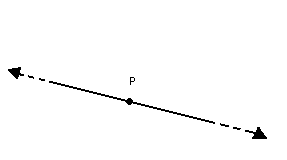
P4) Um ponto qualquer de uma reta divide-a em duas semirretas.

Postulados sobre o plano e o espaço

P5) Por três pontos não-colineares passa um único plano.

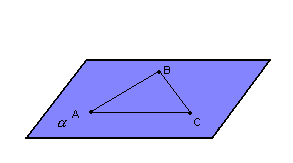
P6) O plano é infinito, isto é, ilimitado.

P7) Por uma reta pode ser traçada uma infinidade de planos.

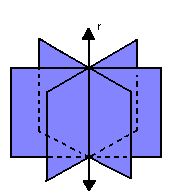
P8) Toda reta pertencente a um plano divide-o em duas regiões chamadas semiplanos.

P9) Qualquer plano divide o espaço em duas regiões chamadas semiespaços.

Posições relativas de duas retas

No espaço, duas retas distintas podem ser concorrentes, paralelas ou reversas:

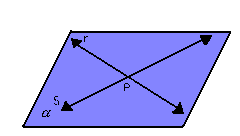
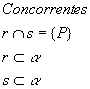
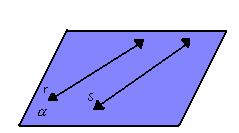
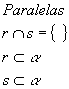
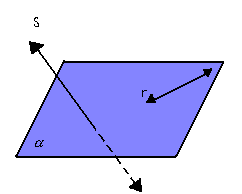
 Temos que considerar dois casos particulares:

• retas perpendiculares: 

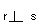
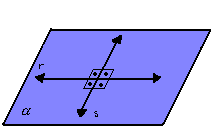
•  retas ortogonais: 
  
  
  

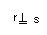
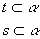
Postulado de Euclides ou das retas paralelas   

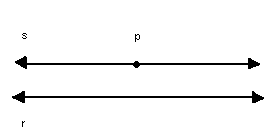
P10) Dados uma reta  r e um ponto P 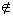 r, existe uma única reta s, traçada por P, tal que r // s:      

Determinação de um plano

Lembrando que, pelo postulado 5, um único plano passa por três pontos não-colineares. Um plano também pode ser determinado por:

• uma reta e um ponto não-pertencente a essa reta:

                                                                                 

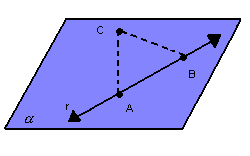
• duas retas distintas concorrentes:

                                                                                     

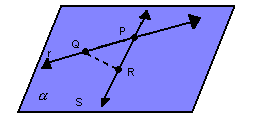
• duas retas paralelas distintas:

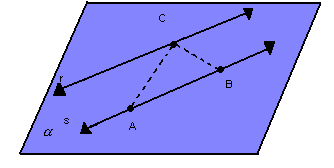
Posições relativas de reta e plano

Vamos considerar as seguintes situações:

a) reta contida no plano: se uma reta r tem dois pontos distintos num plano , então r está contida nesse plano:

b) reta concorrente ou incidente ao plano: dizemos que a reta r "fura" o plano 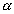 ou que r e  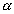são concorrentes em P quando .

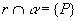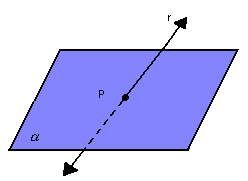
Observação: a reta r é reversa a todas as retas do plano que não passam pelo ponto P.

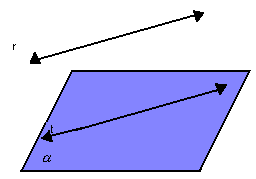
c) reta paralela ao plano: se uma reta r e um plano 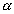 não têm ponto em comum, então a reta r é paralela a uma reta t contida no plano 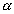; portanto, r // .

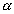Em 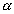 existem infinitas retas paralelas, reversas ou ortogonais a r.

P11) Se dois planos distintos têm um ponto em comum, então a sua intersecção é dada por uma única reta que passa por esse ponto.

Perpendicularismo entre reta e plano

Uma reta r é perpendicular a um plano 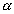 se, e somente se, r é perpendicular a todas as retas de  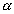que passam pelo ponto de intersecção de r e .

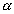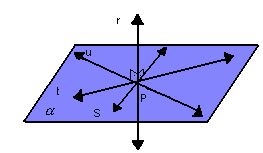
Note que:

• se uma reta r é perpendicular a um plano 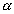, então ela é perpendicular ou ortogonal a toda reta de :

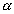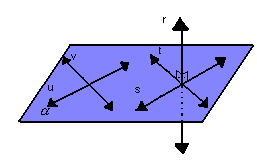
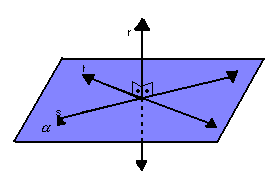
• para que uma reta r seja perpendicular a um plano 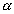, basta ser perpendicular a duas retas concorrentes, contidas em :
  

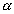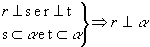
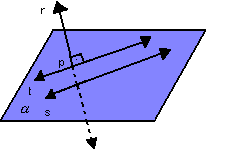
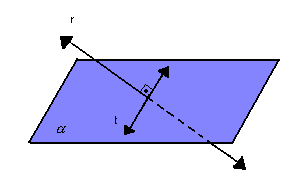
Observe, na figura abaixo, por que não basta que r seja perpendicular a uma única reta t de 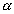 para que seja perpendicular ao plano:

Posições relativas de dois planos

Consideramos as seguintes situações:

a) planos coincidentes ou iguais

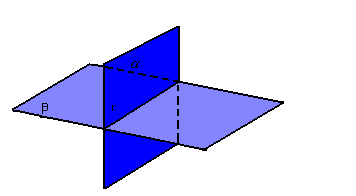
b) planos concorrentes ou secantes

Dois planos, 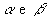, são concorrentes quando sua intersecção é uma única reta:

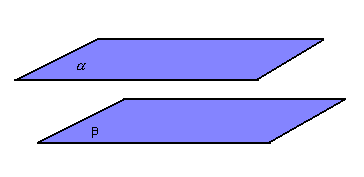
c) planos paralelos

Dois planos, 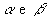, são paralelos quando sua intersecção é vazia:

Perpendicularismo entre planos

Dois planos, 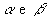, são perpendiculares se, e somente se, existe uma reta de um deles que é perpendicular ao outro:

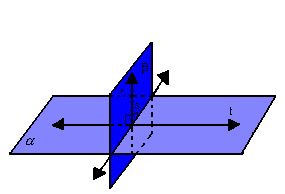
Observação: Existem infinitos planos perpendiculares a um plano dado; esses planos podem ser paralelos entre si ou secantes.