Matemática - Limites
Limites
Noção intuitiva de limite
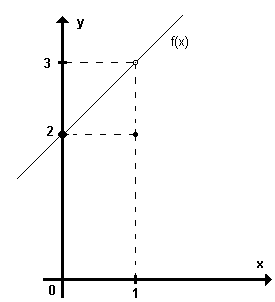
Seja a função f(x)=2x+1. Vamos dar valores a x que se aproximem de 1, pela sua direita (valores maiores que 1) e pela esquerda (valores menores que 1) e calcular o valor correspondente de y:
| x | y = 2x + 1 |
| 1,5 | 4 |
| 1,3 | 3,6 |
| 1,1 | 3,2 |
| 1,05 | 3,1 |
| 1,02 | 3,04 |
| 1,01 | 3,02 |
x
|
y = 2x + 1
|
| 0,5 | 2 |
| 0,7 | 2,4 |
| 0,9 | 2,8 |
| 0,95 | 2,9 |
| 0,98 | 2,96 |
| 0,99 | 2,98 |
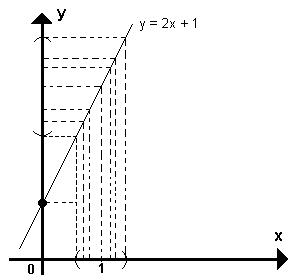
Notamos que à medida que x se aproxima de 1, y se aproxima de 3, ou seja, quando x tende para 1 (x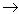 1), y tende para 3 (y
1), y tende para 3 (y 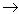 3), ou seja:
3), ou seja:
Observamos que quando x tende para 1, y tende para 3 e o limite da função é 3.
Esse é o estudo do comportamento de f(x) quando x tende para 1 (x 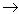 1). Nem é preciso que x assuma o valor 1. Se f(x) tende para 3 (f(x)
1). Nem é preciso que x assuma o valor 1. Se f(x) tende para 3 (f(x) 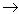 3), dizemos que o limite de f(x) quando x
3), dizemos que o limite de f(x) quando x 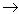 1 é 3, embora possam ocorrer casos em que para x = 1 o valor de f(x) não seja 3. De forma geral, escrevemos:
1 é 3, embora possam ocorrer casos em que para x = 1 o valor de f(x) não seja 3. De forma geral, escrevemos:
se, quando x se aproxima de a (x 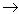 a), f(x) se aproxima de b (f(x)
a), f(x) se aproxima de b (f(x)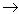 b).
b).
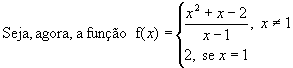
Como x² + x - 2 = (x - 1)(x + 2), temos:
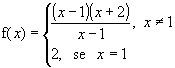
Podemos notar que quando x se aproxima de 1 (x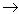 1), f(x) se aproxima de 3, embora para x=1 tenhamos f(x) = 2. o que ocorre é que procuramos o comportamento de y quando x
1), f(x) se aproxima de 3, embora para x=1 tenhamos f(x) = 2. o que ocorre é que procuramos o comportamento de y quando x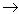 1. E, no caso, y
1. E, no caso, y 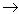 3. Logo, o limite de f(x) é 3.
3. Logo, o limite de f(x) é 3.
Escrevemos:
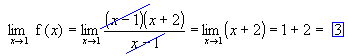
Se g: IR 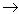 IR e g(x) = x + 2,
IR e g(x) = x + 2, 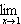 g(x) =
g(x) = 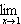 (x + 2) = 1 + 2 = 3, embora g(x)
(x + 2) = 1 + 2 = 3, embora g(x)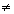 f(x) em x = 1. No entanto, ambas têm o mesmo limite.
f(x) em x = 1. No entanto, ambas têm o mesmo limite.
Propriedades dos limites
1ª) 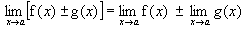
O limite da soma é a soma dos limites.
O limite da diferença é a diferença dos limites.
O limite da diferença é a diferença dos limites.
Exemplo:
2ª) 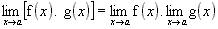
O limite do produto é o produto dos limites.
Exemplo:
3ª) 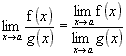
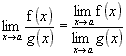
O limite do quociente é o quociente dos limites desde que o denominador não seja zero.
Exemplo:
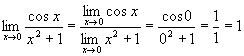
4ª) 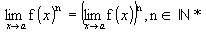
Exemplo:
5ª) 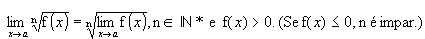
Exemplo:
6ª) 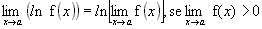
Exemplo:
7ª) 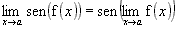
Exemplo:
8ª) 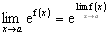
Exemplo:
Limites Laterais
Se x se aproxima de a através de valores maiores que a ou pela sua direita, escrevemos:
Esse limite é chamado de limite lateral à direita de a.
Se x se aproxima de a através de valores menores que a ou pela sua esquerda, escrevemos:
Esse limite é chamado de limite lateral à esquerda de a.
O limite de f(x) para x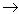 a existe se, e somente se, os limites laterais à direita a esquerda são iguais, ou sejas:
a existe se, e somente se, os limites laterais à direita a esquerda são iguais, ou sejas:
- Se
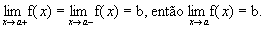
- Se
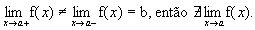
Continuidade
Dizemos que uma função f(x) é contínua num ponto a do seu domínio se as seguintes condições são satisfeitas:
Propriedade das Funções contínuas
Se f(x) e g(x)são contínuas em x = a, então:
- f(x)
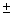 g(x) é contínua em a;
g(x) é contínua em a; - f(x) . g(x) é contínua em a;
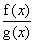 é contínua em a
é contínua em a 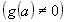 .
.
Limites envolvendo infinito
Conforme sabemos, a expressão:
x 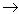
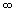 (x tende para infinito)
(x tende para infinito)
significa que x assume valores superiores a qualquer número real e x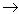
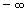 (x tende para menos infinitos), da mesma forma, indica que x assume valores menores que qualquer número real.
(x tende para menos infinitos), da mesma forma, indica que x assume valores menores que qualquer número real.
Exemplo:
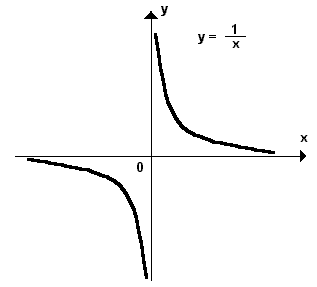
a) 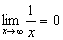 , ou seja, à medida que x aumenta, y tende para zero e o limite é zero.
, ou seja, à medida que x aumenta, y tende para zero e o limite é zero.
b) 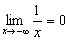 , ou seja, à medida que x diminui, y tende para zero e o limite é zero.
, ou seja, à medida que x diminui, y tende para zero e o limite é zero.
c) 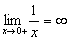 , ou seja, quando x se aproxima de zero pela direita de zero
, ou seja, quando x se aproxima de zero pela direita de zero 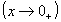 ou por valores maiores que zero, y tende para o infinito e o limite é infinito.
ou por valores maiores que zero, y tende para o infinito e o limite é infinito.
d) 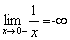 , ou seja, quando x tende para zero pela esquerda ou por valores menores que zero, y tende para menos infinito
, ou seja, quando x tende para zero pela esquerda ou por valores menores que zero, y tende para menos infinito
Limite de uma função polinomial para 
Seja a função polinomial 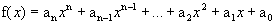 . Então:
. Então:
Demonstração:
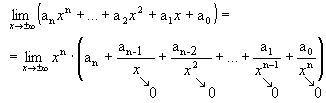
Mas:
Logo:
De forma análoga, para 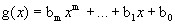 , temos:
, temos:
Exemplos:
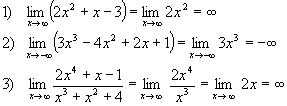
Limites trigonométricos
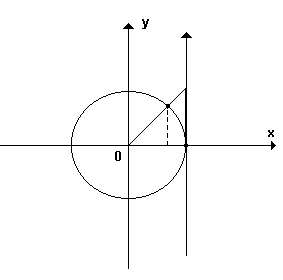
Demonstração:
Para 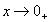 , temos sen x < x < tg x. Dividindo a dupla desigualdade por sen x > 0, vem:
, temos sen x < x < tg x. Dividindo a dupla desigualdade por sen x > 0, vem:
Invertendo, temos:
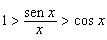
Mas:
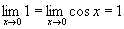
- g(x) < f(x) < h(x) são funções contínuas e se
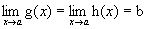 , então,
, então, 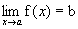 . Logo,
. Logo, 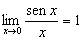
Limites exponenciais
Neste caso, e representa a base dos logaritmos naturais ou neperianos. Trata-se do número irracional e cujo valor aproximado é 2,7182818.
Veja a tabela com valores de x e de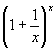 .
.
Veja a tabela com valores de x e de
x
| 1 | 2 | 3 | 10 | 100 | 1 000 | 10 000 | 100 000 |
| 2 | 2,25 | 2,3703 | 2,5937 | 2,7048 | 2,7169 | 2,7181 | 2,7182 |
Notamos que à medida que 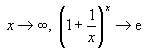 .
.
De forma análoga, efetuando a substituição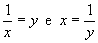 , temos:
, temos:
De forma análoga, efetuando a substituição
Ainda de forma mais geral, temos:
As duas formas acima dão a solução imediata a exercícios deste tipo e evitam substituições algébricas.
Se 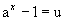 ,então
,então 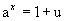 .
.
Mas:
Mas:
Logo:
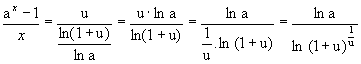
Como x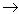 0 , então u
0 , então u 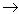 0. Portanto:
0. Portanto:
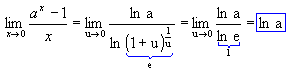
Generalizando a propriedade acima, temos 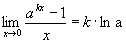 .
.
Comentários
Postar um comentário